Question

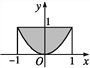
【题目】利用随机模拟方法计算y=x2与y=4围成的面积时,利用计算器产生两组0~1之间的均匀随机数a1=RAND,b1=RAND,然后进行平移与伸缩变换,a=4a1-2,b=4b1,试验进行100次,前98次中落在所求面积区域内的样本点数为65,已知最后两次试验的随机数a1=0.3,b1=0.8及a1=0.4,b1=0.3,那么本次模拟得出的面积的近似值为_____.

Answer 1

【答案】10.72

【解析】由a1=0.3,b1=0.8,得a=-0.8,b=3.2,(-0.8,3.2)落在y=x2与y=4围成的区域内;由a1=0.4,b1=0.3,得a=-0.4,b=1.2,(-0.4,1.2)落在y=x2与y=4围成的区域内,所以本次模拟得出的面积的近似值为16×=10.72.

点睛: 以面积为测度的几何概型问题是几何概型的主要问题，求解与面积有关的几何概型时，关键是弄清某事件对应的面积，必要时可根据题意构造两个变量，把变量看成点的坐标，找到试验全部结果构成的平面图形，以便求解．