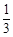题目内容
两个实习生每人加工一个零件,加工为一等品的概率分别为 和
和 ,两个零件是否加工为一等品相互独立,则这两个零件中恰好有一个一等品的概率为( )
,两个零件是否加工为一等品相互独立,则这两个零件中恰好有一个一等品的概率为( )
A. | B. | C. | D. |
B
解析试题分析:根据题意,分析可得,这两个零件中恰有一个一等品包含仅第一个实习生加工一等品与仅第二个实习生加工一等品两种互斥的事件,而两个零件是否加工为一等品相互独立,进而由互斥事件与独立事件的概率计算可得答案.解:记两个零件中恰好有一个一等品的事件为A,即仅第一个实习生加工一等品(A1)与仅第二个实习生加工一等品(A2)两种情况,则P(A)=P(A1)+P(A2)=
 ,故选B.
,故选B.
考点:相互独立事件同时发生的概率
点评:本题考查了相互独立事件同时发生的概率与互斥事件的概率加法公式,解题前,注意区分事件之间的相互关系(对立,互斥,相互独立).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一射手对同一目标独立地射击四次,已知至少命中一次的概率为 ,则此射手每次击中的概率是( )
,则此射手每次击中的概率是( )
A. | B.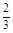 | C. | D. |
今年十一黄金周,记者通过随机询问某景区110名游客对景区的服务是否满意,得到如下的列联表:性别与对景区的服务是否满意 单位:名
| | 男 | 女 | 总计 |
| 满意 | 50 | 30 | 80 |
| 不满意 | 10 | 20 | 30 |
| 总计 | 60 | 50 | 110 |
(2)从(1)中的5名女游客样本中随机选取两名作深度访谈,求选到满意与不满意的女游客各一名的概率;
(3)根据以上列联表,问有多大把握认为“游客性别与对景区的服务满意”有关.
从甲口袋摸出一个红球的概率是 ,从乙口袋中摸出一个红球的概率是
,从乙口袋中摸出一个红球的概率是 ,则
,则 是( )
是( )
| A.2个球不都是红球的概率 | B.2个球都是红球的概率 |
| C.至少有一个红球的概率 | D.2个球中恰好有1个红球的概率 |




 的值等于 ( )
的值等于 ( )
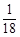


 ,没有平局.采用三局两胜制比赛,即先胜两局者获胜且比赛结束,则甲队获胜的概率等于( )
,没有平局.采用三局两胜制比赛,即先胜两局者获胜且比赛结束,则甲队获胜的概率等于( )

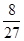



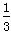


 ,则“出现1点或2点”的概率为( ).
,则“出现1点或2点”的概率为( ).