题目内容
1．在△ABC中，$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{BC}$=$\overrightarrow{b}$，且$\overrightarrow{a}$•$\overrightarrow{b}$＞0，则△ABC为钝角三角形（填“锐角”“直角”或“钝角”）分析 根据向量数量积的定义，可得$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{AB}$||$\overrightarrow{BC}$|•cos（π-∠B）＞0，进而根据诱导公式和余弦的定义，得到结论．
解答 解：∵在△ABC中，$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{BC}$=$\overrightarrow{b}$，
∴$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{AB}$||$\overrightarrow{BC}$|•cos（π-∠B）＞0，
∴cos（π-∠B）＞0，
∴cos∠B＜0，
即B为钝角，
故△ABC为钝角三角形，
故答案为：钝角三角形
点评 本题考查的知识点是三角形形状的判断，平面向量数量积的运算，难度中档．
练习册系列答案
相关题目
11．函数f（x）=sin（ωx+φ）（φ＞0），（-π＜ϕ＜0）的一段图象如图所示，则ϕ=（ ）
| A． | $-\frac{π}{4}$ | B． | $\frac{π}{2}$ | C． | $\frac{π}{4}$ | D． | $-\frac{π}{2}$ |
12．若全集U={0，1，2，3}且∁UA={2}，则集合A为（ ）
| A． | A={0，1} | B． | A={0，1，3} | C． | A={0，1，2，3} | D． | A={1，3} |
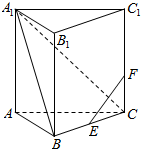如图，已知直三棱柱ABC-A1B1C1的各棱长都是4，E是BC的中点，点F在侧棱CC1上，且CF=1，求证：EF⊥A1C．