题目内容
19.已知a>b>c,用比较法证明:a2b+b2c+c2a>ab2+bc2+ca2.分析 由a>b>c,可得a-b>0,b-c>0,a-c>0,运用作差法,结合因式分解,可得左边-右边=(a-b)(a-c)(b-c)>0,即可得证.
解答 证明:由a>b>c,可得a-b>0,b-c>0,a-c>0,
又a2b+b2c+c2a-ab2-bc2-ca2=(a2b-ab2)+(b2c-ca2)+(c2a-c2b)
=ab(a-b)+c(b-a)(b+a)+c2(a-b)=(a-b)(ab-bc-ac+c2)
=(a-b)(a-c)(b-c)>0,
所以a2b+b2c+c2a>ab2+bc2+ca2.
点评 本题考查不等式的证明,注意运用作差比较法,考查因式分解能力和推理能力,属于基础题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
9.已知全集U={1,2,3,4,5,6,7},M={1,3,5,7},N={2,5,6,7},则M∪(∁UN)=( )
| A. | {1,3,5,7} | B. | {1,2,4} | C. | {1,3,4,5,7} | D. | {1,3,4,5,6} |
9.已知在等差数列{an}满足:a11-a4=4,a3+a7-a10=0,记Sn=a1+a2+…+an,则S13=( )
| A. | 78 | B. | 68 | C. | 56 | D. | 52 |
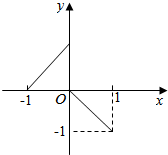 已知函数f(x)的图象如图所示.
已知函数f(x)的图象如图所示.