题目内容
若集合A={(x,y)|x=
},B={(x,y)|y=kx-
k-2},当集合C=A∩B中有两个元素时,实数k的取值范围是( )
| 4-y2 |
| 2 |
分析:集合A表示以原点为圆心,2为半径的半圆,集合B表示恒过(
,-2)的直线方程,画出两函数图象,当直线与圆有两个交点时,两集合的交集有两个元素,专抓住两个关键点:一是直线过(0,2);一是直线与圆相切,分别求出k的值,即可确定出k的范围.
| 2 |
解答: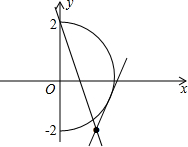 解:集合A中x=
解:集合A中x=
表示以原点为圆心,2为半径的半圆,集合B中y=kx-
k-2表示恒过(
,-2)的直线,画出两函数图象,
当直线过(0,2)时,将(0,2)代入直线方程得:-
k-2=2,即k=-2
;
当直线与圆相切时,圆心到直线的距离d=r,即
=2,
解得:k=2
或k=0(舍去),
则集合C=A∩B中有两个元素时,实数k的取值范围是[-2
,2
).
故选B
 解:集合A中x=
解:集合A中x=| 4-y2 |
| 2 |
| 2 |
当直线过(0,2)时,将(0,2)代入直线方程得:-
| 2 |
| 2 |
当直线与圆相切时,圆心到直线的距离d=r,即
|-
| ||
|
解得:k=2
| 2 |
则集合C=A∩B中有两个元素时,实数k的取值范围是[-2
| 2 |
| 2 |
故选B
点评:此题考查了直线与圆相交的性质,以及交集及其运算,利用了数形结合的思想,熟练掌握数形结合思想是解本题的关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
若集合A={(x,y)|y=
},B={(x,y)|y=k(x-2)},若集合A∩B有两个元素,则实数k的取值范围为( )
| -x2-4x |
A、(-
| ||||||||
B、(-
| ||||||||
C、(-
| ||||||||
D、[-
|