题目内容
经过点F(0,1)且与直线y=-1相切的动圆的圆心轨迹为M.点A、D在轨迹M上,且关于y轴对称,过线段AD(两端点除外)上的任意一点作直线,使直线与轨迹M在点D处的切线平行,设直线与轨迹M交于点B、C.
(1)求轨迹M的方程;
(2)证明:∠BAD=∠CAD;
(3)若点D到直线AB的距离等于
|AD|,且△ABC的面积为20,求直线BC的方程.
(1)求轨迹M的方程;
(2)证明:∠BAD=∠CAD;
(3)若点D到直线AB的距离等于
| ||
| 2 |
分析:(1)设动圆圆心为(x,y),由直线与圆相切可得
=|y+1|,整理即得轨迹M的方程;
(2)由题意,要证∠BAD=∠CAD,可证kAC=-kAB,设点D(x0,
x02),则得kBC=
x0,设点C(x1,
x12),B(x2,
x22),则kBC=
=
x0,化简可得①,由①及斜率公式可得kAC+kAB=0,从而得证;
(3)由点D到AB的距离等于
|AD|,可知∠BAD=45°,不妨设点C在AD上方,即x2<x1,直线AB的方程为:y-
x02=-(x+x0),与抛物线方程联立可得点B的坐标,从而可用x0表示|AB|,同理可表示出|AC|,根据三角形面积为20可解得x0,然后代入求出相应点的坐标,进而可得所求直线方程;
| x2+(y-1)2 |
(2)由题意,要证∠BAD=∠CAD,可证kAC=-kAB,设点D(x0,
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| ||||
| x1-x2 |
| 1 |
| 2 |
(3)由点D到AB的距离等于
| ||
| 2 |
| 1 |
| 4 |
解答:解:(1)设动圆圆心为(x,y),依题意得,
=|y+1|,整理,得x2=4y.
所以轨迹M的方程为x2=4y.
(2)由(1)得x2=4y,即y=
x2,则y′=
x.
设点D(x0,
x02),由导数的几何意义知,直线的斜率为kBC=
x0,
由题意知点A(-x0,
x02).设点C(x1,
x12),B(x2,
x22),
则kBC=
=
=
x0,即x1+x2=2x0,
因为kAC=
=
,kAB=
=
,
由于kAC+kAB=
+
=
=0,即kAC=-kAB,
所以∠BAD=∠CAD;
(3)由点D到AB的距离等于
|AD|,可知∠BAD=45°,
不妨设点C在AD上方,即x2<x1,直线AB的方程为:y-
x02=-(x+x0).
由
,解得点B的坐标为(x0-4,
(x0-4)2),
所以|AB|=
|(x0-4)-(-x0)|=2
|x0-2|.
由(2)知∠BAD=∠CAD=45°,同理可得|AC|=2
|x0+2|,
所以△ABC的面积S=
×2
|x0-2|×2
x0+2|=4|x02-4|=20,解得x0=±3,
当x0=3时,点B的坐标为(-1,
),kBC=
,
直线BC的方程为y-
=
(x+1),即6x-4y+7=0;
当x0=-3时,点B的坐标为(-7,
),kBC=-
,
直线BC的方程为y-
=-
(x+7),即6x+4y-7=0.
| x2+(y-1)2 |
所以轨迹M的方程为x2=4y.
(2)由(1)得x2=4y,即y=
| 1 |
| 4 |
| 1 |
| 2 |
设点D(x0,
| 1 |
| 4 |
| 1 |
| 2 |
由题意知点A(-x0,
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
则kBC=
| ||||
| x1-x2 |
| x1+x2 |
| 4 |
| 1 |
| 2 |
因为kAC=
| ||||
| x1+x0 |
| x1-x0 |
| 4 |
| ||||
| x2+x0 |
| x2-x0 |
| 4 |
由于kAC+kAB=
| x1-x0 |
| 4 |
| x2-x0 |
| 4 |
| (x1+x2)-2x0 |
| 4 |
所以∠BAD=∠CAD;
(3)由点D到AB的距离等于
| ||
| 2 |
不妨设点C在AD上方,即x2<x1,直线AB的方程为:y-
| 1 |
| 4 |
由
|
| 1 |
| 4 |
所以|AB|=
| 2 |
| 2 |
由(2)知∠BAD=∠CAD=45°,同理可得|AC|=2
| 2 |
所以△ABC的面积S=
| 1 |
| 2 |
| 2 |
| 2| |
当x0=3时,点B的坐标为(-1,
| 1 |
| 4 |
| 3 |
| 2 |
直线BC的方程为y-
| 1 |
| 4 |
| 3 |
| 2 |
当x0=-3时,点B的坐标为(-7,
| 49 |
| 4 |
| 3 |
| 2 |
直线BC的方程为y-
| 49 |
| 4 |
| 3 |
| 2 |
点评:本小题主要考查动点的轨迹和直线与圆锥曲线的位置关系、导数的几何意义等基础知识,考查运算求解能力和推理论证能力等.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
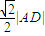 ,且△ABC的面积为20,求直线BC的方程.
,且△ABC的面积为20,求直线BC的方程.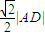 ,且△ABC的面积为20,求直线BC的方程.
,且△ABC的面积为20,求直线BC的方程.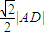 ,且△ABC的面积为20,求直线BC的方程.
,且△ABC的面积为20,求直线BC的方程.