题目内容
经过点F (0,1)且与直线y=-1相切的动圆的圆心轨迹为M点A、D在轨迹M上,且关于y轴对称,过线段AD (两端点除外)上的任意一点作直线l,使直线l与轨迹M 在点D处的切线平行,设直线l与轨迹M交于点B、C.(1)求轨迹M的方程;
(2)证明:∠BAD=∠CAD;
(3)若点D到直线AB的距离等于
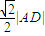 ,且△ABC的面积为20,求直线BC的方程.
,且△ABC的面积为20,求直线BC的方程.
【答案】分析:(1)设出动圆的圆心坐标,利用动圆经过定点F(0,1),且与定直线:y=-1相切,列出方程化简即可得到所求轨迹方程.
(2)由(1)得y= x2,设D(x,
x2,设D(x,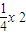 ),由导数的几何意义,得直线l的斜率,又A(-x,
),由导数的几何意义,得直线l的斜率,又A(-x,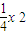 ),设C(x1,
),设C(x1,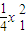 ),B(x2,
),B(x2,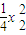 ).利用斜率公式得到x1+x2=2x.从而有kAB=-kBC,即可证得∠BAD=∠CAD.
).利用斜率公式得到x1+x2=2x.从而有kAB=-kBC,即可证得∠BAD=∠CAD.
(3)根据条件:点D到直线AB的距离等于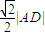 ,可知∠BAD=45°,将直线AB的方程与x2=-4y联立方程组,解得B点的坐标,求出|AB|,|AC|,最后根据△ABC的面积列出方程,解得x=±3,从而得出直线BC的方程.
,可知∠BAD=45°,将直线AB的方程与x2=-4y联立方程组,解得B点的坐标,求出|AB|,|AC|,最后根据△ABC的面积列出方程,解得x=±3,从而得出直线BC的方程.
解答:解:(1)设圆心坐标为(x,y),由题意动圆经过定点F(0,1),且与定直线:y=-1相切,
所以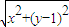 =|y+1|,
=|y+1|,
即(y-1)2+x2=(y+1)2,
即x2=4y.故轨迹M的方程为x2=4y.
(2)由(1)得y= x2,∴y′=
x2,∴y′= x,
x,
设D(x,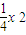 ),由导数的几何意义 得直线l的斜率为kBC=
),由导数的几何意义 得直线l的斜率为kBC=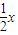 ,
,
则A(-x,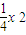 ),设C(x1,
),设C(x1,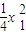 ),B(x2,
),B(x2,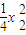 ).
).
则kBC=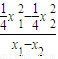 =
=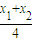 =
= x,∴x1+x2=2x.
x,∴x1+x2=2x.
kAC=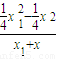 =
=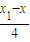 ,kAB=
,kAB=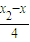 ,
,
∴kBC+AB=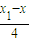 +
+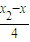 =
=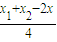 =0,∴kAB=-kBC.
=0,∴kAB=-kBC.
∴∠BAD=∠CAD.
(3)点D到直线AB的距离等于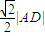 ,可知∠BAD=45°,
,可知∠BAD=45°,
不妨设C在AD上方,即x2<x1,直线AB的方程为:y-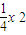 =-(x+x),与x2=-4y联立方程组,
=-(x+x),与x2=-4y联立方程组,
解得B点的坐标为(x-4,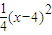 ),∴|AB|=
),∴|AB|=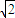 |x-4-(-x)|=2
|x-4-(-x)|=2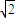 |x-2|
|x-2|
由(2)知,∠CAD=∠BAD=45°,同理可得|AC|=2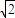 |x+2|.
|x+2|.
∴△ABC的面积为 ×
×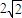 |x+2|×2
|x+2|×2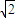 |x-2|=20.
|x-2|=20.
解得x=±3.
当x=3时,B((-1, ),KBC=
),KBC= ,直线BC的方程为6x-4y+7=0;
,直线BC的方程为6x-4y+7=0;
当x=-3时,B((-7,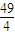 ),KBC=-
),KBC=- ,直线BC的方程为6x+4y-7=0;
,直线BC的方程为6x+4y-7=0;
点评:本题是中档题,考查动点的轨迹方程的求法,直线与抛物线的位置关系,考查计算能力.
(2)由(1)得y=
 x2,设D(x,
x2,设D(x,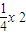 ),由导数的几何意义,得直线l的斜率,又A(-x,
),由导数的几何意义,得直线l的斜率,又A(-x,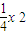 ),设C(x1,
),设C(x1,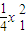 ),B(x2,
),B(x2,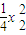 ).利用斜率公式得到x1+x2=2x.从而有kAB=-kBC,即可证得∠BAD=∠CAD.
).利用斜率公式得到x1+x2=2x.从而有kAB=-kBC,即可证得∠BAD=∠CAD.(3)根据条件:点D到直线AB的距离等于
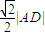 ,可知∠BAD=45°,将直线AB的方程与x2=-4y联立方程组,解得B点的坐标,求出|AB|,|AC|,最后根据△ABC的面积列出方程,解得x=±3,从而得出直线BC的方程.
,可知∠BAD=45°,将直线AB的方程与x2=-4y联立方程组,解得B点的坐标,求出|AB|,|AC|,最后根据△ABC的面积列出方程,解得x=±3,从而得出直线BC的方程.解答:解:(1)设圆心坐标为(x,y),由题意动圆经过定点F(0,1),且与定直线:y=-1相切,
所以
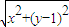 =|y+1|,
=|y+1|,即(y-1)2+x2=(y+1)2,
即x2=4y.故轨迹M的方程为x2=4y.
(2)由(1)得y=
 x2,∴y′=
x2,∴y′= x,
x,设D(x,
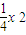 ),由导数的几何意义 得直线l的斜率为kBC=
),由导数的几何意义 得直线l的斜率为kBC=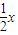 ,
,则A(-x,
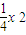 ),设C(x1,
),设C(x1,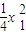 ),B(x2,
),B(x2,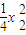 ).
).则kBC=
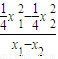 =
=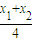 =
= x,∴x1+x2=2x.
x,∴x1+x2=2x.kAC=
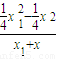 =
=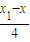 ,kAB=
,kAB=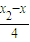 ,
,∴kBC+AB=
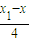 +
+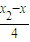 =
=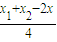 =0,∴kAB=-kBC.
=0,∴kAB=-kBC.∴∠BAD=∠CAD.
(3)点D到直线AB的距离等于
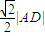 ,可知∠BAD=45°,
,可知∠BAD=45°,不妨设C在AD上方,即x2<x1,直线AB的方程为:y-
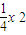 =-(x+x),与x2=-4y联立方程组,
=-(x+x),与x2=-4y联立方程组,解得B点的坐标为(x-4,
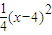 ),∴|AB|=
),∴|AB|=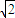 |x-4-(-x)|=2
|x-4-(-x)|=2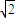 |x-2|
|x-2|由(2)知,∠CAD=∠BAD=45°,同理可得|AC|=2
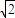 |x+2|.
|x+2|.∴△ABC的面积为
 ×
×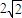 |x+2|×2
|x+2|×2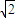 |x-2|=20.
|x-2|=20.解得x=±3.
当x=3时,B((-1,
 ),KBC=
),KBC= ,直线BC的方程为6x-4y+7=0;
,直线BC的方程为6x-4y+7=0;当x=-3时,B((-7,
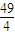 ),KBC=-
),KBC=- ,直线BC的方程为6x+4y-7=0;
,直线BC的方程为6x+4y-7=0;点评:本题是中档题,考查动点的轨迹方程的求法,直线与抛物线的位置关系,考查计算能力.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
已知动圆C经过点F(0,1),并且与直线y=-1相切,若直线3x-4y+20=0与圆C有公共点,则圆C的面积( )
| A、有最大值为π | B、有最小值为π | C、有最大值为4π | D、有最小值为4π |
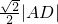 ,且△ABC的面积为20,求直线BC的方程.
,且△ABC的面积为20,求直线BC的方程.