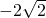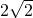题目内容
将圆O:x2+y2=4上各点的纵坐标变为原来的一半(横坐标不变),得到曲线C.设O为坐标原点,直线l:x=my+
与C交于A、B两点,N为线段AB的中点,延长线段ON交C于点E.若
=2
,则m=( )
| 3 |
| OE |
| ON |
分析:根据圆O:x2+y2=4上各点的纵坐标变为原来的一半(横坐标不变),将圆O中y换为2y,变形后得到曲线C的方程,设A(x1,y1,B(x2,y2),将曲线C与圆O方程联立,消去x得到关于y的一元二次方程,利用根与系数的关系表示出y1+y2,再由N为AB的中点,利用中点公式表示出N的纵坐标,将N纵坐标代入直线l方程中表示出横坐标,确定出N的坐标,由
=2
,得到E的坐标,将E坐标代入曲线C方程中,得到关于m的方程,求出方程的解即可得到m的值.
| OE |
| ON |
解答: 解:将圆O:x2+y2=4上各点的纵坐标变为原来的一半(横坐标不变),
解:将圆O:x2+y2=4上各点的纵坐标变为原来的一半(横坐标不变),
得到曲线C方程为x2+4y2=4,
设A(x1,y1),B(x2,y2),
将直线l与曲线C方程联立得:
,
消去x得:(m2+4)y2+2
my-1=0,
∴y1+y2=-
,
又N为AB的中点,设N(x0,y0),
∴y0=
=-
,
将y0=
代入方程得:x=m•(-
)+
=
,
∴N(
,-
),
∵
=2
,
∴E(
,-
),
将E坐标代入x2+4y2=4得:(
)2+4(-
)2=4,
整理得:m4-4m2-32=0,
∴m2=8或m2=-4(舍去),
则m=±2
.
故选D
 解:将圆O:x2+y2=4上各点的纵坐标变为原来的一半(横坐标不变),
解:将圆O:x2+y2=4上各点的纵坐标变为原来的一半(横坐标不变),得到曲线C方程为x2+4y2=4,
设A(x1,y1),B(x2,y2),
将直线l与曲线C方程联立得:
|
消去x得:(m2+4)y2+2
| 3 |
∴y1+y2=-
2
| ||
| m2+4 |
又N为AB的中点,设N(x0,y0),
∴y0=
| y1+y2 |
| 2 |
| ||
| m2+4 |
将y0=
| ||
| m2+4 |
| ||
| m2+4 |
| 3 |
4
| ||
| m2+4 |
∴N(
4
| ||
| m2+4 |
| ||
| m2+4 |
∵
| OE |
| ON |
∴E(
8
| ||
| m2+4 |
2
| ||
| m2+4 |
将E坐标代入x2+4y2=4得:(
8
| ||
| m2+4 |
2
| ||
| m2+4 |
整理得:m4-4m2-32=0,
∴m2=8或m2=-4(舍去),
则m=±2
| 2 |
故选D
点评:此题考查了圆与椭圆方程的变换,椭圆与直线的位置关系,韦达定理,线段中点坐标公式,以及平面向量的数量积运算,是一道综合性较强的试题.

练习册系列答案
相关题目
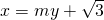 与C交于A、B两点,N为线段AB的中点,延长线段ON交C于点E.若
与C交于A、B两点,N为线段AB的中点,延长线段ON交C于点E.若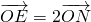 ,则m=
,则m=