题目内容
在高二年级某班学生在数学校本课程选课过程中,已知第一小组与第二小组各有六位同学.每位同学都只选了一个科目,第一小组选《数学运算》的有1人,选《数学解题思想与方法》的有5人,第二小组选《数学运算》的有2人,选《数学解题思想与方法》的有4人,现从第一、第二两小组各任选2人分析选课情况.(Ⅰ)求选出的4人均选《数学解题思想与方法》的概率;
(Ⅱ)设ξ为选出的4个人中选《数学运算》的人数,求ξ的分布列和数学期望.
分析:(Ⅰ)求选出的4人均选《数学解题思想与方法》的概率.故可以设“从第一小组选出的2人选《数学解题思想与方法》”为事件A,“从第二小组选出的2人选《数学解题思想与方法》”为事件B.分别求出事件A、B发生的概率,然后根据相互独立事件的概率乘法公式即可得到答案.
(Ⅱ)求ξ的分布列和数学期望,因为ξ可能的取值为0,1,2,3.分别求出每个取值的概率,即可得到分布列,然后根据期望公式求解即可.
(Ⅱ)求ξ的分布列和数学期望,因为ξ可能的取值为0,1,2,3.分别求出每个取值的概率,即可得到分布列,然后根据期望公式求解即可.
解答:解:(Ⅰ)设“从第一小组选出的2人选《数学解题思想与方法》”为事件A,“从第二小组选出的2人选《数学解题思想与方法》”为事件B.由于事件A、B相互独立,且P(A)=
=
,P(B)=
=
.
所以选出的4人均考《数学解题思想与方法》的概率为P(A•B)=P(A)•P(B)=
×
=
(Ⅱ)设ξ可能的取值为0,1,2,3.得
P(ξ=0)=
P(ξ=1)=
•
+
•
═
P(ξ=3)=
•
=
P(ξ=2)=1-P(ξ=0)-P(ξ=1)-P(ξ=3)=
,
ξ的分布列
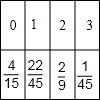 ∴ξ的数学期望Eξ=0×
∴ξ的数学期望Eξ=0×
+1×
+2×
+3×
=1
| ||
|
| 2 |
| 3 |
| ||
|
| 2 |
| 5 |
所以选出的4人均考《数学解题思想与方法》的概率为P(A•B)=P(A)•P(B)=
| 2 |
| 3 |
| 2 |
| 5 |
| 4 |
| 15 |
(Ⅱ)设ξ可能的取值为0,1,2,3.得
P(ξ=0)=
| 4 |
| 15 |
P(ξ=1)=
| ||
|
| ||||
|
| ||
|
| ||
|
| 22 |
| 45 |
P(ξ=3)=
| ||
|
| 1 | ||
|
| 1 |
| 45 |
P(ξ=2)=1-P(ξ=0)-P(ξ=1)-P(ξ=3)=
| 2 |
| 9 |
ξ的分布列
 ∴ξ的数学期望Eξ=0×
∴ξ的数学期望Eξ=0×| 4 |
| 15 |
| 22 |
| 45 |
| 2 |
| 9 |
| 1 |
| 45 |
点评:此题主要考查离散型随机变量的分布列和期望的求法,其中涉及到相互独立事件的概率乘法公式的应用.考查概率问题在实际中的应用,有一定的灵活性.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目