题目内容
已知数列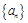 的首项
的首项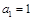 ,前n项之和
,前n项之和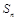 满足关系式:
满足关系式: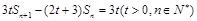 .
.
(1)求证:数列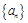 是等比数列;
是等比数列;
(2)设数列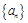 的公比为
的公比为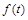 ,数列
,数列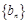 满足
满足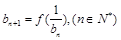 ,且
,且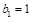 .
.
(i)求数列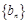 的通项
的通项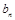 ;
;
(ii)设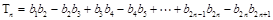 ,求
,求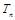 .
.
【答案】
(1)见解析 (2)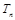
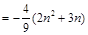
【解析】(1) 本小题的求解思路:先出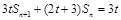 ,得
,得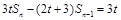 (
(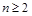 ),∴
),∴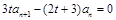 ,∴
,∴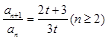 ,然后再由a1,求出a2,如果
,然后再由a1,求出a2,如果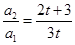 ,那么就说明数列
,那么就说明数列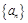 是等比数列.否则就不是.
是等比数列.否则就不是.
(2)(i)根据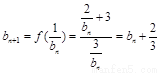 ,确定{bn}是等差数列,从而求出其通项公式.
,确定{bn}是等差数列,从而求出其通项公式.
(ii)在(i)的基础b2n-1,b2n,从而可知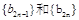 都是以
都是以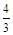 为公差的等差数列,
为公差的等差数列,
所以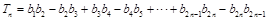
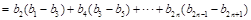
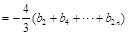 问题到此基本得到解决
问题到此基本得到解决
(1)证明: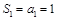 ,
,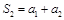 得
得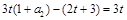 ∴
∴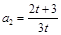 ∴
∴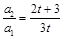 …(2分)∵
…(2分)∵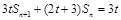
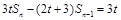 (
(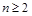 )
)
∴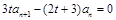 ∴
∴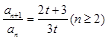 …………(5分)又∵
…………(5分)又∵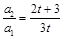
∴数列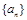 是以1为首项.
是以1为首项.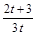 为公比的等比数列……………(6分)
为公比的等比数列……………(6分)
(2)(ⅰ)解: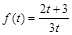 ∴
∴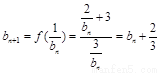 而
而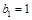
∴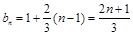 ………………(9分)
………………(9分)
(ⅱ)∵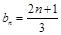 ∴
∴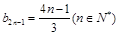
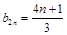
∴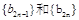 都是以
都是以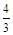 为公差的等差数列. ∴
为公差的等差数列. ∴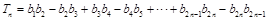
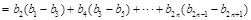
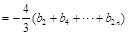
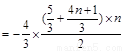
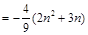

练习册系列答案
相关题目


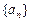 的首项
的首项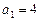 ,前n项和为Sn,且
,前n项和为Sn,且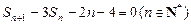 .
. ,
,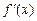 是函数
是函数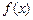 的导函数,求
的导函数,求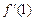 .
.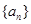 的首项
的首项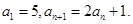
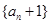 是等比数列;
是等比数列;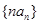 的前n项和为
的前n项和为 ,试比较
,试比较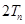 与
与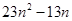 的大小。
的大小。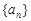 的首项
的首项 ,前n项和为Sn ,且
,前n项和为Sn ,且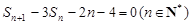 .
.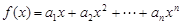 ,
,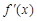 是函数
是函数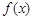 的导函数,求
的导函数,求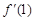 .
.