题目内容
在平面直角坐标系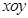 中,圆
中,圆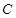 的方程为
的方程为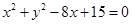 ,若直线
,若直线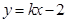 上至少存在一点,使得以该点为圆心,
上至少存在一点,使得以该点为圆心,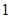 为半径的圆与圆
为半径的圆与圆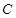 有公共点,则
有公共点,则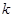 的最大值为
的最大值为
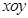 中,圆
中,圆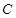 的方程为
的方程为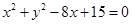 ,若直线
,若直线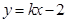 上至少存在一点,使得以该点为圆心,
上至少存在一点,使得以该点为圆心,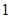 为半径的圆与圆
为半径的圆与圆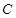 有公共点,则
有公共点,则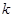 的最大值为
的最大值为 A.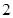 | B.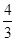 | C.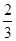 | D.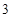 |
B
试题分析:∵圆C的方程可化为:
 ,∴圆C的圆心为
,∴圆C的圆心为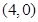 ,半径为1。
,半径为1。∵由题意,直线
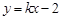 上至少存在一点
上至少存在一点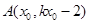 ,以该点为圆心,1为半径的圆与圆
,以该点为圆心,1为半径的圆与圆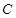 有公共点;∴存在
有公共点;∴存在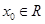 ,使得
,使得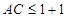 成立,即
成立,即 。∵
。∵ 即为点
即为点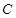 到直线
到直线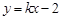 的距离
的距离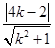 ,∴
,∴ ,解得
,解得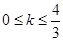 。∴
。∴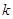 的最大值是
的最大值是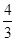 。
。点评:解题的关键是通过分析将题设条件转化为圆心到直线的距离不超过2从而建立不等式,最后确定出范围

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
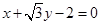 被圆
被圆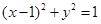 截得的线段的长为( )
截得的线段的长为( )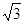
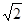
 .设该圆过点H(3,5)的两条弦分别为AC和BD,且
.设该圆过点H(3,5)的两条弦分别为AC和BD,且 .则四边形ABCD的面积最大值为( )
.则四边形ABCD的面积最大值为( )

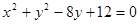 ,直线
,直线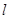 :
: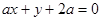 .
.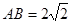 时,求直线
时,求直线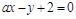 与圆
与圆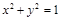 相切,则实数
相切,则实数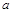 的值为 .
的值为 .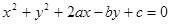 表示圆心为C(2,2),半径为2的圆,则
表示圆心为C(2,2),半径为2的圆,则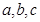 的值依次为 ( )
的值依次为 ( ) 、4、4;
、4、4;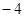 、4;
、4;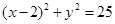 的弦AB的中点,则直线AB的方程为( )
的弦AB的中点,则直线AB的方程为( )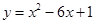 与坐标轴的交点都在圆上,则于昂的方程为_________________.
与坐标轴的交点都在圆上,则于昂的方程为_________________.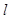 过点
过点 与圆
与圆 相切,
相切,