题目内容
[番茄花园1] 如图,在平行四边形ABCD中,AB=2BC,∠ABC=120°。E为线段AB的中点,将△ADE沿直线DE翻折成△A’DE,使平面A’DE⊥平面BCD,F为线段A’C的中点。
(Ⅰ)求证:BF∥平面A’DE;
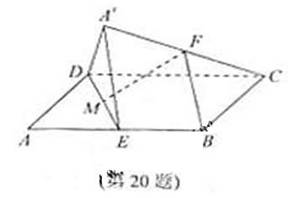 (Ⅱ)设M为线段DE的中点,求直线FM与平面A’DE所成角的余弦值。
(Ⅱ)设M为线段DE的中点,求直线FM与平面A’DE所成角的余弦值。
[番茄花园1]1.
【答案】
[番茄花园1] 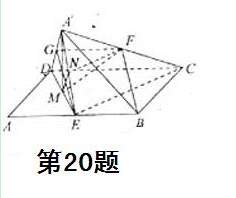 .解析:本题主要考查空间线线、线面、面面位置关系,线面角等基础知识,同时考查空间想象能力和推理论证能力。
.解析:本题主要考查空间线线、线面、面面位置关系,线面角等基础知识,同时考查空间想象能力和推理论证能力。
(Ⅰ)证明:取A′D的中点G,连结GF,CE,由条件易知
FG∥CD,FG=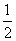 CD.
CD.
BE∥CD,BE=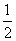 CD.
CD.
所以FG∥BE,FG=BE.
故四边形BEGF为平行四边形,
所以BF∥EG
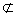 因为
因为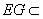 平面
平面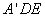 ,BF
,BF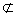 平面
平面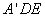
所以 BF//平面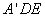
(Ⅱ)解:在平行四边形,ABCD中,设BC=a
则AB=CD=2a, AD=AE=EB=a,
连CE
因为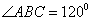
在△BCE中,可得CE=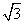 a,
a,
在△ADE中,可得DE=a,
在△CDE中,因为CD2=CE2+DE2,所以CE⊥DE,
在正三角形A′DE中,M为DE中点,所以A′M⊥DE.
由平面A′DE⊥平面BCD,
可知A′M⊥平面BCD,A′M⊥CE.
取A′E的中点N,连线NM、NF,
所以NF⊥DE,NF⊥A′M.
因为DE交A′M于M,
所以NF⊥平面A′DE,
则∠FMN为直线FM与平面A′DE新成角.
在Rt△FMN中,NF=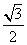 a,
MN=
a,
MN=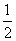 a,
FM=a,
a,
FM=a,
则cos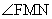 =
=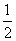 .
.
所以直线FM与平面A′DE所成角的余弦值为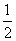 .
.
证明:存在实数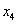 ,使得
,使得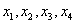 按某种顺序排列后的等差数列,并求
按某种顺序排列后的等差数列,并求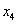
[番茄花园1]20.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 如图,质点
如图,质点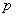 在半径为2的圆周上逆时针运动,其初始位置为
在半径为2的圆周上逆时针运动,其初始位置为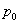 (
(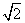 ,
,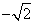 ),角速度为1,那么点
),角速度为1,那么点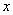 轴距离
轴距离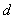 关于时间
关于时间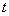 的函数图像大致为
的函数图像大致为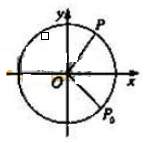
 如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P0(
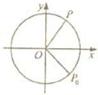
如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P0(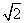 ,-
,-
 如图,二面角
如图,二面角 的大小是60°,线段
的大小是60°,线段 .
. ,
, 与
与 所成的角为30°.则
所成的角为30°.则 所成的角的正弦值是
.
所成的角的正弦值是
.