题目内容
设M点的坐标为(x,y).
(1)设集合P={-4,-3,-2,0},Q={0,1,2},从集合P中随机取一个数作为x,从集合Q中取随机取一个数作为y,求M点落在y轴的概率;
(2)设x∈[0,3],y∈[0,4],求点M落在不等式组:
,所表示的平面区域内的概率
【答案】
(1)记“M点落在y轴”为事件A.
M点的组成情况共4×3=12种,且每种情况出现的可能性相等,属于古典概型.
其中事件A包含的基本事件有(0,0),(0,1),(0,2)共3处.
∴P(A)==.
(2)依条件可知,点M均匀地分布在不等式组所表示的平面区域内,属于几何概型.该平面区域的图形为右图中矩形OABC围成的区域,面积为S=3×4=12.
而所求事件构成的平面区域
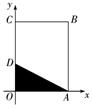
由不等式组表示的区域,其图形如右图中的三角形OAD(阴影部分).
又直线x+2y-3=0与x轴、y轴的交点分别为A(3,0)、D,
∴三角形OAD的面积为
S1=×3×=.
∴所求事件的概率为P===.
【解析】略

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
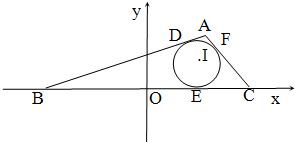 如图,△ABC的内切圆与三边AB、BC、CA的切点分别为D、E、F,已知B(-
如图,△ABC的内切圆与三边AB、BC、CA的切点分别为D、E、F,已知B(-