题目内容
正整数按下列方法分组：{1}，{2，3，4}，{5，6，7，8，9}，{10，11，12，13，14，15，16}，…，记第n组各数之和为An；由自然数的立方构成下列数组：{03，13}，{13，23}，{23，33}，{33，43}，…，记第n组中两数之和为Bn，则An-Bn= ．
【答案】分析：观察已知数列的特点可知，每个数组有2n-1个数，且这些数构成以1为公差的等差数列，且每组数的最后一个数为n2，根据等差数列的前n和公式可求An，而Bn=（n-1）3+n3，利用立方和公式进行变形，从而可求
解答：解：由题意可得，第n组数据构成以1为公差的等差数列，共有2n-1个数，且最后一个数位n2
则由等差数列的通项公式可得第n组数的第一个数为：n2-2n+2
由等差数列的前n项和公式可得，
Bn=（n-1）3+n3=（2n-1）[（（n-1）2-n（n-1）+n2]=（2n-1）（n2-n+1）
An-Bn=0
故答案为：0
点评：本题主要考查了等差数列的和公式在求和中的应用，解题的关键是根据已知所给的数组观察发现正整数组中，第n组数据构成以1为公差的等差数列，共有2n-1个数，且最后一个数位n2．
解答：解：由题意可得，第n组数据构成以1为公差的等差数列，共有2n-1个数，且最后一个数位n2
则由等差数列的通项公式可得第n组数的第一个数为：n2-2n+2
由等差数列的前n项和公式可得，
Bn=（n-1）3+n3=（2n-1）[（（n-1）2-n（n-1）+n2]=（2n-1）（n2-n+1）
An-Bn=0
故答案为：0
点评：本题主要考查了等差数列的和公式在求和中的应用，解题的关键是根据已知所给的数组观察发现正整数组中，第n组数据构成以1为公差的等差数列，共有2n-1个数，且最后一个数位n2．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
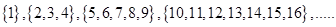记第
组中各数之和为
；由自然数的立方构成下列数组：
记第
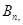则
．
，
，
，
，……，
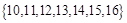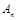；由自然数的立方构成下列数组：
，
，
，
，……，
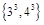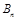，则
．