题目内容
.已知“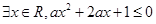 ”为假命题,则实数a的取值范围是 。
”为假命题,则实数a的取值范围是 。
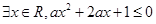 ”为假命题,则实数a的取值范围是 。
”为假命题,则实数a的取值范围是 。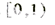
分析:根据已知中“?x∈R,ax2+2ax+1≤0”为假命题,我们可以得到否定命题,“?x∈R,ax2+2ax+1>0”为真命题,则问题可转化为一个函数恒成立问题,对二次项系数a分类讨论后,综合讨论结果,即可得到答案.
解:∵“?x∈R,ax2+2ax+1≤0”为假命题,
∴其否定“?x∈R,ax2+2ax+1>0”为真命题,
当a=0时,显然成立;
当a≠0时,ax2+2ax+1>0恒成立可化为:
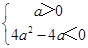
解得0<a<1
综上实数a的取值范围是[0,1)
故答案为:[0,1)

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 的角一定是锐角
的角一定是锐角 上的角可以表示为
上的角可以表示为 ,
,
 ,则角
,则角 的正切值等于角
的正切值等于角 的正切值
的正切值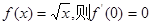
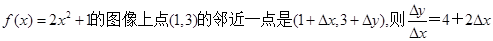
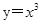 在点(0,0)处没有切线
在点(0,0)处没有切线 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,则下列命题正确的是
是两个不同的平面,则下列命题正确的是 ,则
,则
 则
则
 则
则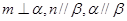 ,则
,则
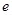 越大、椭圆越接近圆;q:双曲线的离心率
越大、椭圆越接近圆;q:双曲线的离心率

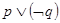

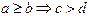 ”和“
”和“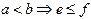 ”都是假命题,其逆命题都是真命题,则“
”都是假命题,其逆命题都是真命题,则“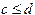 ”是“
”是“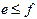 ”的( ).
”的( ). 

 ,则
,则 :对任意的
:对任意的
 ,使
,使 成立
成立