题目内容
12.若实数x,y满足|x-1|-ln$\frac{1}{y}$=0,则y关于x的函数图象的大致形状是( )| A. |  | B. | 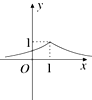 | C. | 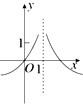 | D. | 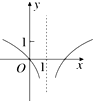 |
分析 先化简函数的解析式,函数中含有绝对值,故可先去绝对值讨论,结合指数函数的单调性及定义域、对称性,即可选出答案.
解答 解:∵|x-1|-ln$\frac{1}{y}$=0,
∴f(x)=($\frac{1}{e}$)|x-1|
其定义域为R,当x≥1时,f(x)=($\frac{1}{e}$)x-1,因为0<$\frac{1}{e-1}$<1,故为减函数,
又因为f(x)的图象关于x=1轴对称,
对照选项,只有B正确.
故选:B.
点评 本题考查指数函数的图象问题、考查识图能力,属于基础题.

练习册系列答案
相关题目
19.函数y=4-ax+1(a>0,a≠1)的图象必过定点,这个定点是( )
| A. | (0,4) | B. | (1,3) | C. | (-1,3) | D. | (0,1) |
3.全班48名学生坐成6排,每排8人,排法总数为P,排成前后两排,每排24人,排法总数为Q,则有( )
| A. | P>Q | B. | P=Q | C. | P<Q | D. | 不能确定 |
20.已知x、y是实数,则“xy=0”是“x2+y2=0”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
17.已知tanθ=4,$\frac{1+cos2θ+8si{n}^{2}θ}{sin2θ}$的值是( )
| A. | $\frac{20\sqrt{3}}{3}$ | B. | $\frac{65}{4}$ | C. | 4 | D. | 4$\sqrt{2}$ |
1.实数x,y满足:$\left\{\begin{array}{l}x≥1\\ x+y≤3\\ y≥\frac{1}{2}(x-3)\end{array}\right.$,则z=2x+y的最小值为( )
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |