题目内容
某校为了规范教职工绩效考核制度,现准备拟定一函数用于根据当月评价分数 (正常情况
(正常情况 ,且教职工平均月评价分数在50分左右,若有突出贡献可以高于100分)计算当月绩效工资
,且教职工平均月评价分数在50分左右,若有突出贡献可以高于100分)计算当月绩效工资 元.要求绩效工资不低于500元,不设上限且让大部分教职工绩效工资在600元左右,另外绩效工资越低、越高人数要越少.则下列函数最符合要求的是( )
元.要求绩效工资不低于500元,不设上限且让大部分教职工绩效工资在600元左右,另外绩效工资越低、越高人数要越少.则下列函数最符合要求的是( )
A.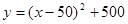 | B. |
C. | D. |
C.
解析试题分析:由题意知,函数应满足单调增,且先慢后快,在 左右增长缓慢,最小值为500,A是先减后增差误,B由指数函数知是增长越来越快,D由对数函数增长速度越来越慢.C是
左右增长缓慢,最小值为500,A是先减后增差误,B由指数函数知是增长越来越快,D由对数函数增长速度越来越慢.C是 的平移和伸缩变换而得,故最符合题目要求,故选C.
的平移和伸缩变换而得,故最符合题目要求,故选C.
考点:函数模型及其应用.

练习册系列答案
相关题目
设 ,则在下列区间中,使函数
,则在下列区间中,使函数 有零点的区间是( )
有零点的区间是( )
A. | B. | C. | D. |
设函数 ,则方程
,则方程 的根有( )
的根有( )
| A.1个 | B. 2个 | C.3个 | D.无数个 |
已知定义域为R的函数 ,若关于
,若关于 的方程
的方程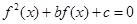 有3个不同的实根
有3个不同的实根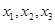 ,则
,则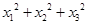 等于( )
等于( )
| A.13 | B.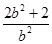 | C.5 | D.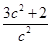 |
已知 是
是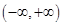 上的增函数,则实数
上的增函数,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知函数 ,则方程
,则方程 的解集是( )
的解集是( )
A.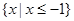 | B. |
C. 或 或 | D. 或 或 |
设实数 ,则
,则 的大小关系为
的大小关系为
A. | B. |
C. | D. |
已知数列 满足
满足 且
且 是函数
是函数 的两个零点,则
的两个零点,则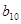 等于( )
等于( )
| A.24 | B.32 | C.48 | D.64 |
 和函数
和函数 的图象恒过同一个定点,且该定点始终落在圆
的图象恒过同一个定点,且该定点始终落在圆 的内部或圆上,那么
的内部或圆上,那么 的取值范围是 ( )
的取值范围是 ( )