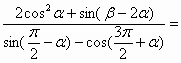题目内容
已知向量| a |
| b |
| 3 |
| a |
| b |
分析：利用向量共线的坐标形式的充要条件列出方程求出tanα，据特殊角的三角函数值求出角．
解答：解：∵
∥
，
∴tanα-
=0，即tanα=
，
又α∈（0，π），
∴α=
．
故答案为
| a |
| b |
∴tanα-
| 3 |
| 3 |
又α∈（0，π），
∴α=
| π |
| 3 |
故答案为
| π |
| 3 |
点评：本题考查向量共线的坐标形式的充要条件；特殊的三角函数值．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
β)，－1)向量b＝(cosα，2)若
为f(x)＝cos(2x＋
)的最小正周期，且a·b＝2，则
，其中
∈
求
,tan(
+
)),b=(
sin(
+
),tan(
-
)),令f(x)=a·b,求函数f(x)的最大值、最小正周期,并写出f(x)在［0,π］上的单调区间. 
,tan(
+
)),b=(
sin(
+
),tan(
-
)),令(x)=a·b.求函数f(x)的最大值，最小正周期，并写出f(x)在［0，π］上的单调区间.