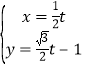题目内容
【题目】已知点P不在直线l、m上,则“过点P可以作无数个平面,使得直线l、m都与这些平面平行”是“直线l、m互相平行”的( )
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分也不必要条件
【答案】C
【解析】
根据直线和平面平行的性质,结合充分条件和必要条件的定义进行判断即可.
![]() 点
点![]() 不在直线
不在直线![]() 、
、![]() 上,
上,
![]() 若直线
若直线![]() 、
、![]() 互相平行,则过点
互相平行,则过点![]() 可以作无数个平面,使得直线
可以作无数个平面,使得直线![]() 、
、![]() 都与这些平面平行,即必要性成立,
都与这些平面平行,即必要性成立,
若过点![]() 可以作无数个平面,使得直线
可以作无数个平面,使得直线![]() 、
、![]() 都与这些平面平行,则直线
都与这些平面平行,则直线![]() 、
、![]() 互相平行成立,反证法证明如下:
互相平行成立,反证法证明如下:
若直线![]() 、
、![]() 互相不平行,则
互相不平行,则![]() ,
,![]() 异面或相交,则过点
异面或相交,则过点![]() 只能作一个平面同时和两条直线平行,则与条件矛盾,即充分性成立
只能作一个平面同时和两条直线平行,则与条件矛盾,即充分性成立
则“过点![]() 可以作无数个平面,使得直线
可以作无数个平面,使得直线![]() 、
、![]() 都与这些平面平行”是“直线
都与这些平面平行”是“直线![]() 、
、![]() 互相平行”的充要条件,
互相平行”的充要条件,
故选:![]() .
.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
【题目】 已知参赛号码为1~4号的四名射箭运动员参加射箭比赛。
(1)通过抽签将他们安排到1~4号靶位,试求恰有一名运动员所抽靶位号与其参赛号码相同的概率;
(2)记1号,2号射箭运动员,射箭的环数为![]() (
(![]() 所有取值为0,1,2,3...,10)。
所有取值为0,1,2,3...,10)。
根据教练员提供的资料,其概率分布如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0 | 0 | 0 | 0 | 0.06 | 0.04 | 0.06 | 0.3 | 0.2 | 0.3 | 0.04 |
| 0 | 0 | 0 | 0 | 0.04 | 0.05 | 0.05 | 0.2 | 0.32 | 0.32 | 0.02 |
- 若1,2号运动员各射箭一次,求两人中至少有一人命中8环的概率;
- 判断1号,2号射箭运动员谁射箭的水平高?并说明理由.
【题目】
|
某商场经销某商品,根据以往资料统计,顾客采用的付款期数![]() 的分布列为
的分布列为
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为250元;分4期或5期付款,其利润为300元.![]() 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(Ⅰ)求事件A:“购买该商品的3位顾客中,至少有1位采用1期付款”的概率
P(A);
(Ⅱ)求![]() 的分布列及期望
的分布列及期望![]()