题目内容
已知直线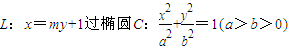 的右焦点F,且交椭圆C于A,B两点.
的右焦点F,且交椭圆C于A,B两点.(1)若抛物线
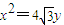 的焦点为椭圆C的上顶点,求椭圆C的方程;
的焦点为椭圆C的上顶点,求椭圆C的方程;(2)对于(1)中的椭圆C,若直线L交y轴于点M,且
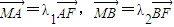 ,当m变化时,求λ1+λ2的值.
,当m变化时,求λ1+λ2的值.
【答案】分析:(1)根据抛物线 的焦点为(0,
的焦点为(0,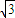 ),且为椭圆C的上顶点,可得b2=3,又F(1,0),可得c=1,从而可得a2=b2+c2=4,故可求椭圆C的方程;
),且为椭圆C的上顶点,可得b2=3,又F(1,0),可得c=1,从而可得a2=b2+c2=4,故可求椭圆C的方程;
(2)l与y轴交于 ,设A(x1,y1),B(x2,y2),则由
,设A(x1,y1),B(x2,y2),则由 可得:(3m2+4)y2+6my-9=0,故△=144(m2+1)>0,利用韦达定理可得
可得:(3m2+4)y2+6my-9=0,故△=144(m2+1)>0,利用韦达定理可得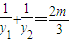 ,根据
,根据 ,可得
,可得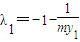 ,同理
,同理 ,从而可求λ1+λ2的值.
,从而可求λ1+λ2的值.
解答:解:(1)抛物线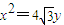 的焦点为(0,
的焦点为(0,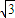 ),且为椭圆C的上顶点
),且为椭圆C的上顶点
∴ ,∴b2=3,
,∴b2=3,
又F(1,0),∴c=1,a2=b2+c2=4.
∴椭圆C的方程为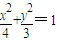 .
.
(2)l与y轴交于 ,设A(x1,y1),B(x2,y2),则
,设A(x1,y1),B(x2,y2),则
由 可得:(3m2+4)y2+6my-9=0,故△=144(m2+1)>0.
可得:(3m2+4)y2+6my-9=0,故△=144(m2+1)>0.
∴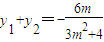 ,
,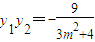
∴ .
.
又由 ,得
,得 .
.
∴ .
.
同理 .
.
∴ .
.
点评:本题考查椭圆的标准方程,考查直线与椭圆相交,考查向量知识的运用,解题的关键是联立方程组,利用韦达定理解题.
 的焦点为(0,
的焦点为(0,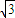 ),且为椭圆C的上顶点,可得b2=3,又F(1,0),可得c=1,从而可得a2=b2+c2=4,故可求椭圆C的方程;
),且为椭圆C的上顶点,可得b2=3,又F(1,0),可得c=1,从而可得a2=b2+c2=4,故可求椭圆C的方程;(2)l与y轴交于
 ,设A(x1,y1),B(x2,y2),则由
,设A(x1,y1),B(x2,y2),则由 可得:(3m2+4)y2+6my-9=0,故△=144(m2+1)>0,利用韦达定理可得
可得:(3m2+4)y2+6my-9=0,故△=144(m2+1)>0,利用韦达定理可得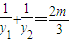 ,根据
,根据 ,可得
,可得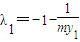 ,同理
,同理 ,从而可求λ1+λ2的值.
,从而可求λ1+λ2的值.解答:解:(1)抛物线
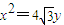 的焦点为(0,
的焦点为(0,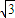 ),且为椭圆C的上顶点
),且为椭圆C的上顶点∴
 ,∴b2=3,
,∴b2=3,又F(1,0),∴c=1,a2=b2+c2=4.
∴椭圆C的方程为
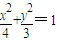 .
.(2)l与y轴交于
 ,设A(x1,y1),B(x2,y2),则
,设A(x1,y1),B(x2,y2),则由
 可得:(3m2+4)y2+6my-9=0,故△=144(m2+1)>0.
可得:(3m2+4)y2+6my-9=0,故△=144(m2+1)>0.∴
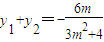 ,
,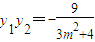
∴
 .
.又由
 ,得
,得 .
.∴
 .
.同理
 .
.∴
 .
.点评:本题考查椭圆的标准方程,考查直线与椭圆相交,考查向量知识的运用,解题的关键是联立方程组,利用韦达定理解题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目

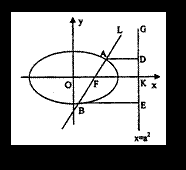
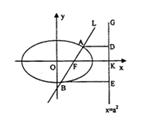
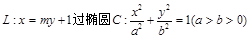 的右焦点F,且交椭圆C于A,B两点.
的右焦点F,且交椭圆C于A,B两点.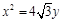 的焦点为椭圆C的上顶点,求椭圆C的方程;
的焦点为椭圆C的上顶点,求椭圆C的方程;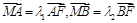 ,当m变化时,求
,当m变化时,求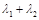 的值.
的值.