题目内容
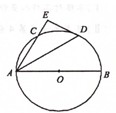如图，AB是圆O的直径，AC是弦，∠BAC的平分线AD交圆O于点D，DE⊥AC且交AC的延长线于点E．求证：DE是圆O的切线．
分析：根据OA=OD，得到∠ODA=∠OAD，结合AD是∠BAC的平分线，得到∠OAD=∠DAC=∠ODA，可得OD∥AE．再根据DE⊥AE，得到DE⊥OD，结合圆的切线的判定定理，得到DE是⊙O的切线．
解答：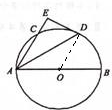
证明：连接OD，
∵OA=OD，∴∠ODA=∠OAD
∵∠BAC的平分线是AD
∴∠OAD=∠DAC
∴∠DAC=∠ODA，可得OD∥AE…（5分）
又∵DE⊥AE，∴DE⊥OD
∵OD是⊙O的半径
∴DE是⊙O的切线．…（10分）
证明：连接OD，∵OA=OD，∴∠ODA=∠OAD
∵∠BAC的平分线是AD
∴∠OAD=∠DAC
∴∠DAC=∠ODA，可得OD∥AE…（5分）
又∵DE⊥AE，∴DE⊥OD
∵OD是⊙O的半径
∴DE是⊙O的切线．…（10分）
点评：本题以角平分线和圆中的垂直线段为载体，通过证明圆的切线，考查了圆的切线的判定定理等知识点，属于中档题．
练习册系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
如图，直三棱柱的一个底面ABC内接于圆O，AB是圆O的直径．
与直线
的夹角大小为
B．（不等式选讲）要使关于x的不等式
在实数