题目内容
已知O为原点,向量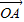 =(3cosx,3sinx),
=(3cosx,3sinx),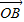 =(3cosx,sinx),
=(3cosx,sinx),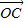 =(2,0),x
=(2,0),x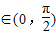 .
.(1)求证:(
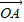 -
-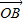 )
)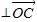 ;
;(2)求tan∠AOB的最大值及相应x值.
【答案】分析:(1)先求出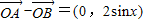 ,再由(
,再由(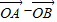 )•
)•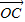 =0×2+2sinx×0=0可证.
=0×2+2sinx×0=0可证.
(2)由tan∠AOB=tan(∠AOC-∠BOC),根据两角差的正切公式可得答案.
解答:解:(1)∵0<x<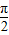 ,∴3sinx>sinx,∴
,∴3sinx>sinx,∴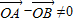
又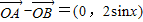
∴(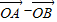 )•
)•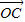 =0×2+2sinx×0=0
=0×2+2sinx×0=0
∴(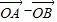 )⊥
)⊥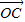 .
.
(2)tan∠AOC=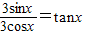 ,tan
,tan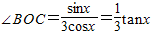
∵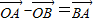 ,∴
,∴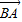 ⊥
⊥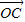 ,0<
,0<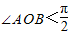 .
.
∴tan∠AOB=tan(∠AOC-∠BOC)
=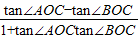 =
=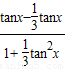
=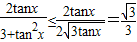
(当tanx=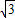 即x=
即x=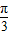 时取“=”)
时取“=”)
所以tan∠AOB的最大值为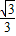 ,相应的x=
,相应的x=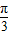
点评:本题主要考查向量垂直和点乘之间的关系以及三角的正切求值问题.
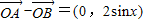 ,再由(
,再由(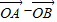 )•
)•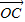 =0×2+2sinx×0=0可证.
=0×2+2sinx×0=0可证.(2)由tan∠AOB=tan(∠AOC-∠BOC),根据两角差的正切公式可得答案.
解答:解:(1)∵0<x<
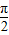 ,∴3sinx>sinx,∴
,∴3sinx>sinx,∴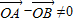
又
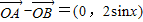
∴(
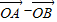 )•
)•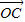 =0×2+2sinx×0=0
=0×2+2sinx×0=0∴(
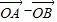 )⊥
)⊥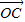 .
.(2)tan∠AOC=
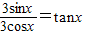 ,tan
,tan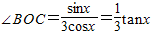
∵
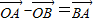 ,∴
,∴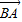 ⊥
⊥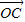 ,0<
,0<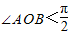 .
.∴tan∠AOB=tan(∠AOC-∠BOC)
=
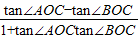 =
=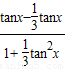
=
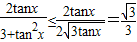
(当tanx=
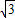 即x=
即x=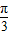 时取“=”)
时取“=”)所以tan∠AOB的最大值为
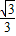 ,相应的x=
,相应的x=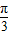
点评:本题主要考查向量垂直和点乘之间的关系以及三角的正切求值问题.

练习册系列答案
相关题目
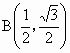 ,则
,则