题目内容
 一个水平放置的△ABC用斜二测画法画出的直观图是如图2-7-3所示的边长为1的正△A'B'C',则在真实图形中AB边上的高是
一个水平放置的△ABC用斜二测画法画出的直观图是如图2-7-3所示的边长为1的正△A'B'C',则在真实图形中AB边上的高是| 6 |
| 6 |
| ||
| 2 |
| ||
| 2 |
| ||
| 4 |
| ||
| 4 |
分析:根据斜二测画法的原理,将正三角形放入锐角为45°的斜角坐标系内,作C'D'⊥A'B'于D'并将其还原为图(2)的△ABC.利用解三角形知识算出O'C'=
,从而得到真实图形中△ABC的高等于
,进而得到△ABC的面积,算出直观图和真实图形的面积的比值.
| ||
| 2 |
| 6 |
解答:解:将正△A'B'C'放入锐角为45°的斜角坐标系x'o'y'内,如图(1)所示,
过C'作C'D'⊥A'B',垂足为D'
将其还原为真实图形,得到图(2)的△ABC
其中OA=O'A',AB=A'B',OC=2O'C'
在△OC'D'中,O'C'=
=
∴真实图形中,OC=
,即△ABC的高等于
由此可得△ABC的面积S=
×1×
=
∵直观图中正△A'B'C'的面积为
∴直观图和真实图形的面积的比值等于
=
故答案为:
,
,
过C'作C'D'⊥A'B',垂足为D'

将其还原为真实图形,得到图(2)的△ABC
其中OA=O'A',AB=A'B',OC=2O'C'
在△OC'D'中,O'C'=
| CD |
| sin45° |
| ||
| 2 |
∴真实图形中,OC=
| 6 |
| 6 |
由此可得△ABC的面积S=
| 1 |
| 2 |
| 6 |
| ||
| 2 |
∵直观图中正△A'B'C'的面积为
| ||
| 4 |
∴直观图和真实图形的面积的比值等于
| ||||
|
| ||
| 4 |
故答案为:
| 6 |
| ||
| 2 |
| ||
| 4 |
点评:本题给出一个三角形的直观图是边长为1的正三角形,求原图形的高和面积.着重考查了解三角形、斜二测画法的原理等知识,属于中档题.

练习册系列答案
相关题目
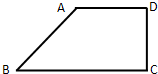 一个水平放置的平面图形的斜二测直观图是直角梯形(如图)∠ABC=45°,AB=AD=1,DC⊥BC,则这个平面图形的面积为
一个水平放置的平面图形的斜二测直观图是直角梯形(如图)∠ABC=45°,AB=AD=1,DC⊥BC,则这个平面图形的面积为 一个水平放置的平面图形,其斜二测直观图是一个等腰三角形,腰AB=AC=1,如图,则平面图形的实际面积为( )
一个水平放置的平面图形,其斜二测直观图是一个等腰三角形,腰AB=AC=1,如图,则平面图形的实际面积为( ) 一个水平放置的平面图形的斜二测直观图是直角梯形ABCD,如图所示,∠ABC=45°,AB=AD=1,DC⊥BC,这个平面图形的面积为
一个水平放置的平面图形的斜二测直观图是直角梯形ABCD,如图所示,∠ABC=45°,AB=AD=1,DC⊥BC,这个平面图形的面积为