题目内容
 已知PA⊥平面ABCD,PA=AB=AD=2,AC与BD交于E点,BD=2,BC=CD.
已知PA⊥平面ABCD,PA=AB=AD=2,AC与BD交于E点,BD=2,BC=CD.(1)取PD中点F,求证:PB∥平面AFC.
(2)求二面角A-PB-E的余弦值.
【答案】分析:(1)利用空间坐标系解.先以AC、AP分别为y、z轴,A为原点,建立如图所示空间直角坐标系,欲证PB∥平面ACF,只须证PB∥EF,分别求出向量的坐标后,结合向量的线性运算即可进行判断.
(2)欲求二面角A-PB-E的余弦值,只须求出平面PAB、平面PBE的法向量的夹角,再结合图形求其补角即得.
解答: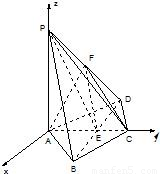 解:以AC、AP分别为y、z轴,A为原点,建立如图所示空间直角坐标系,
解:以AC、AP分别为y、z轴,A为原点,建立如图所示空间直角坐标系,
∵PA=AB=AD=BD=2,BC=CD,
∴△ABC≌△ADC,
∴△ABD是等边三角形,且E是BD中点,AC⊥BD,
则A(0,0,0)、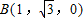 、
、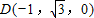 、
、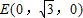 、P(0,0,2)、
、P(0,0,2)、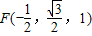
(1)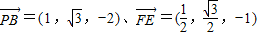 ,
,
∴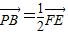 ,
,
∴PB∥EF,
∴PB∥平面ACF.
(2)设平面PAB、平面PBE的法向量分别为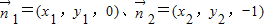 ,
,
则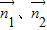 的夹角的补角就是二面角A-PB-E的平面角.
的夹角的补角就是二面角A-PB-E的平面角.
∵ ,
, ,
,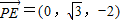 ,
,
由 及
及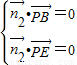
得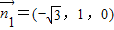 ,
,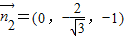 .
.
∴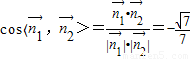 ,
,
∴二面角A-PB-E的余弦值为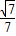 .
.
点评:本题主要考查了异面直线及其所成的角,以及直线与平面平行的判定等知识,还考查了空间想象力、空间向量的运算.属于基础题.
(2)欲求二面角A-PB-E的余弦值,只须求出平面PAB、平面PBE的法向量的夹角,再结合图形求其补角即得.
解答:
 解:以AC、AP分别为y、z轴,A为原点,建立如图所示空间直角坐标系,
解:以AC、AP分别为y、z轴,A为原点,建立如图所示空间直角坐标系,∵PA=AB=AD=BD=2,BC=CD,
∴△ABC≌△ADC,
∴△ABD是等边三角形,且E是BD中点,AC⊥BD,
则A(0,0,0)、
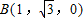 、
、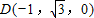 、
、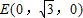 、P(0,0,2)、
、P(0,0,2)、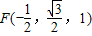
(1)
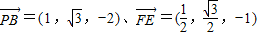 ,
,∴
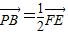 ,
,∴PB∥EF,
∴PB∥平面ACF.
(2)设平面PAB、平面PBE的法向量分别为
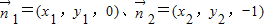 ,
,则
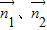 的夹角的补角就是二面角A-PB-E的平面角.
的夹角的补角就是二面角A-PB-E的平面角.∵
 ,
, ,
,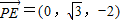 ,
,由
 及
及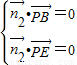
得
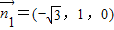 ,
,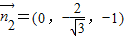 .
.∴
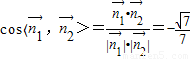 ,
,∴二面角A-PB-E的余弦值为
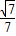 .
.点评:本题主要考查了异面直线及其所成的角,以及直线与平面平行的判定等知识,还考查了空间想象力、空间向量的运算.属于基础题.

练习册系列答案
相关题目
 如图,三棱锥P-ABC中,已知PA⊥平面ABC,PA=3,PB=PC=BC=6,求二面角P-BC-A的正弦值.
如图,三棱锥P-ABC中,已知PA⊥平面ABC,PA=3,PB=PC=BC=6,求二面角P-BC-A的正弦值. (2012•宝鸡模拟)如图,已知PA⊥平面ABC,且
(2012•宝鸡模拟)如图,已知PA⊥平面ABC,且 (2012•徐汇区一模)如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D,E分别是BC,AP的中点.
(2012•徐汇区一模)如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D,E分别是BC,AP的中点. (2012•徐汇区一模)如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D是AB的中点.
(2012•徐汇区一模)如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D是AB的中点. (2013•盐城三模)如图,三棱锥P-ABC中,已知PA⊥平面ABC,△ABC是边长为2的正三角形,D,E分别为PB,PC中点.
(2013•盐城三模)如图,三棱锥P-ABC中,已知PA⊥平面ABC,△ABC是边长为2的正三角形,D,E分别为PB,PC中点.