题目内容
如图所示,五面体ABCDE中,正 ABC的边长为1,AE
ABC的边长为1,AE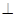 平面ABC,CD∥AE,且CD=
平面ABC,CD∥AE,且CD= AE.
AE.
(I)设CE与平面ABE所成的角为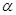 ,AE=
,AE= 若
若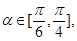 求
求 的取值范围;
的取值范围;
(Ⅱ)在(I)和条件下,当 取得最大值时,求平面BDE与平面ABC所成角的大小.
取得最大值时,求平面BDE与平面ABC所成角的大小.

【答案】

解:方法一:
(Ⅰ)取 中点
中点 ,连结
,连结 、
、 ,由
,由 为正三角形,得
为正三角形,得 ,又
,又 ,则
,则 ,可知
,可知 ,所以
,所以 为
为 与平面
与平面 所成角.……………2分
所成角.……………2分
 ,……………4分
,……………4分
因为 ,得
,得 ,得
,得 .……………6分
.……………6分
(Ⅱ)延长 交于点S,连
交于点S,连 ,
,
可知平面
 平面
平面 =
= .………………………7分
.………………………7分
由 ,且
,且 ,又因为
,又因为 =1,从而
=1,从而 ,…………………8分
,…………………8分
又 面
面 ,由三垂线定理可知
,由三垂线定理可知 ,即
,即 为平面
为平面 与平面
与平面 所成的角;……………………10分
所成的角;……………………10分
则 ,
,
从而平面 与面
与面 所成的角的大小为
所成的角的大小为 .………………12分
.………………12分
方法二:
 解:
解:
(Ⅰ)如图以C为坐标原点,CA、CD为y、z轴,垂直于CA、CD的直线CT为x轴,建立空间直角坐标系(如图),则
设 ,
, ,
, ,
, .……………2分
.……………2分
取AB的中点M,则 ,
,
易知,ABE的一个法向量为 ,
,
由题意 .………………4分
.………………4分
由 ,则
,则
 ,ww..com
,ww..com
得 .…………………6分
.…………………6分
(Ⅱ)由(Ⅰ)知 最大值为
最大值为 ,则当
,则当 时,设平面BDE法向量为
时,设平面BDE法向量为 ,则
,则
取 ,………………8分
,………………8分
又平面ABC法向量为 ,……………………10分
,……………………10分
所以 =
= ,
,
所以平面BDE与平面ABC所成角大小 ……………………12分
……………………12分
【解析】略

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 如图所示的五面体中,四边形ABCD是矩形,DA⊥面ABEF,且DA=1,AB∥EF,AB=
如图所示的五面体中,四边形ABCD是矩形,DA⊥面ABEF,且DA=1,AB∥EF,AB= 如图所示的五面体中,四边形ABCD是矩形,DA⊥面ABEF,M为EF中点,且DA=1,AB∥EF,AB=
如图所示的五面体中,四边形ABCD是矩形,DA⊥面ABEF,M为EF中点,且DA=1,AB∥EF,AB= (2)当AB1//平面BDC1时,求二面角C-BC1-D的余弦值
(2)当AB1//平面BDC1时,求二面角C-BC1-D的余弦值
 EF=2
EF=2 ,AF=BE=2.
,AF=BE=2.