题目内容
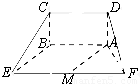
如图所示的五面体中,四边形ABCD是矩形,DA⊥面ABEF,M为EF中点,且DA=1,AB∥EF,AB= EF=2
EF=2 ,AF=BE=2.
,AF=BE=2.(Ⅰ)求证:CM∥平面ADF;
(Ⅱ)求三棱锥M-ADF的体积.

【答案】分析:(I)利用平行四边形的判定定理和性质定理、线面平行的判定定理即可得出;
(II)利用已知可证:△FAM为直角三角形且∠FAM=90°.利用DA⊥面ABEF,且DA=1,可得DA是三棱锥D-MAF的高.
可得VM-ADF=VD-MAF= .
.
解答:(I)证明:连接CM,由题意可得,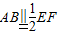 ,
, ,MF=
,MF= ,
,
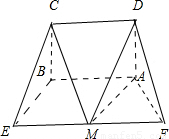 ∴
∴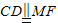 ,
,
∴四边形MFDC为平行四边形,
∴DF∥CM.
∵DF?平面ADF,CM?平面ADF,
∴CM∥平面ADF.
(Ⅱ)解:∵M为EF的中点,
∴EM=AB=2 ,
,
又∵AB∥EF,∴四边形ABEM是平行四边形.
∴AM=BE=2,
又∵AF=2,MF=2 ,
,
∴△FAM为直角三角形且∠FAM=90°.
∴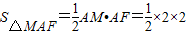 =2.
=2.
∵DA⊥面ABEF,且DA=1,∴DA是三棱锥D-MAF的高.
∴VM-ADF=VD-MAF= =
=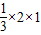 =
= .
.
点评:熟练掌握平行四边形的判定定理和性质定理、线面平行的判定定理、线面垂直的性质、三棱锥的体积计算公式、等体积变形等是解题的关键.
(II)利用已知可证:△FAM为直角三角形且∠FAM=90°.利用DA⊥面ABEF,且DA=1,可得DA是三棱锥D-MAF的高.
可得VM-ADF=VD-MAF=
 .
.解答:(I)证明:连接CM,由题意可得,
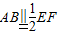 ,
, ,MF=
,MF= ,
, ∴
∴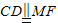 ,
,∴四边形MFDC为平行四边形,
∴DF∥CM.
∵DF?平面ADF,CM?平面ADF,
∴CM∥平面ADF.
(Ⅱ)解:∵M为EF的中点,
∴EM=AB=2
 ,
,又∵AB∥EF,∴四边形ABEM是平行四边形.
∴AM=BE=2,
又∵AF=2,MF=2
 ,
,∴△FAM为直角三角形且∠FAM=90°.
∴
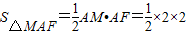 =2.
=2.∵DA⊥面ABEF,且DA=1,∴DA是三棱锥D-MAF的高.
∴VM-ADF=VD-MAF=
 =
=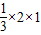 =
= .
.点评:熟练掌握平行四边形的判定定理和性质定理、线面平行的判定定理、线面垂直的性质、三棱锥的体积计算公式、等体积变形等是解题的关键.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 如图所示的五面体中,四边形ABCD是矩形,DA⊥面ABEF,且DA=1,AB∥EF,AB=
如图所示的五面体中,四边形ABCD是矩形,DA⊥面ABEF,且DA=1,AB∥EF,AB= 如图所示的五面体中,四边形ABCD是矩形,DA⊥面ABEF,M为EF中点,且DA=1,AB∥EF,AB=
如图所示的五面体中,四边形ABCD是矩形,DA⊥面ABEF,M为EF中点,且DA=1,AB∥EF,AB=
 EF=2
EF=2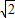 ,AF=BE=2.
,AF=BE=2.