题目内容
已知f(z)=z-︱2+z︱,且f( )=4-3i,求复数z.
)=4-3i,求复数z.
 )=4-3i,求复数z.
)=4-3i,求复数z.解:设z=a+bi (a,b∈R)
则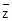 = a-bi
= a-bi
∵f(z)="z" -︱2+z︱, f(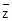 )=4-3i
)=4-3i
∴f(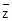 )=
)=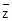 -∣2+
-∣2+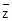 ∣= a-bi-∣2+a-bi∣
∣= a-bi-∣2+a-bi∣
=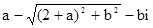 =4-3i
=4-3i
由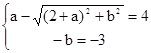 得:
得: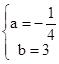
∴复数z =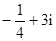 ----------12分
----------12分
则
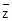 = a-bi
= a-bi∵f(z)="z" -︱2+z︱, f(
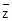 )=4-3i
)=4-3i∴f(
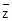 )=
)=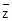 -∣2+
-∣2+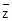 ∣= a-bi-∣2+a-bi∣
∣= a-bi-∣2+a-bi∣=
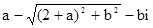 =4-3i
=4-3i由
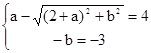 得:
得: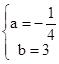
∴复数z =
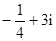 ----------12分
----------12分本试题主要是考查了复数的运算以及复数的概念的运用。利用设z=a+bi (a,b∈R)
则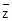 = a-bi且f(z)=z-︱2+z︱,且f(
= a-bi且f(z)=z-︱2+z︱,且f( )=4-3i,,那么利用复数相等可知参数a,b的值得到结论。
)=4-3i,,那么利用复数相等可知参数a,b的值得到结论。
则
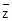 = a-bi且f(z)=z-︱2+z︱,且f(
= a-bi且f(z)=z-︱2+z︱,且f( )=4-3i,,那么利用复数相等可知参数a,b的值得到结论。
)=4-3i,,那么利用复数相等可知参数a,b的值得到结论。
练习册系列答案
相关题目
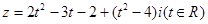 为纯虚数,则t的值为 。
为纯虚数,则t的值为 。 为复数,
为复数, 和
和 均为实数,其中
均为实数,其中 是虚数单位.
是虚数单位. 在复平面上对应的点在第一象限,求实数
在复平面上对应的点在第一象限,求实数 的取值范围.
的取值范围.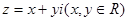 ,则满足
,则满足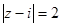 的复数
的复数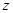 的轨迹是圆;
的轨迹是圆;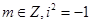 ,则
,则




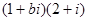 是纯虚数(
是纯虚数(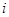 是虚数单位,
是虚数单位,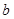 是实数),则
是实数),则



 为虚数单位,复数
为虚数单位,复数 ,则复数
,则复数 的虚部是___ .
的虚部是___ . 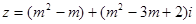 是纯虚数,则实数
是纯虚数,则实数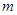 =________
=________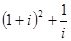 的值=___.
的值=___. ,其中
,其中 、
、
 ,
, 是
是 虚数单位,则
虚数单位,则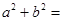 _________。
_________。