题目内容
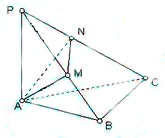
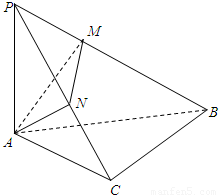
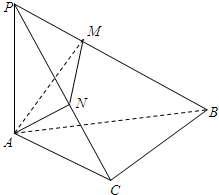 如图所示,在斜边为AB的Rt△ABC中,过A作PA⊥平面ABC,AM⊥PB于M,
如图所示,在斜边为AB的Rt△ABC中,过A作PA⊥平面ABC,AM⊥PB于M,AN⊥PC于N.(Ⅰ)求证:BC⊥面PAC;
(Ⅱ)求证:PB⊥面AMN.
(Ⅲ)若PA=AB=4,设∠BPC=θ,试用tanθ表示△AMN 的面积,当tanθ取何值时,△AMN的面积最大?最大面积是多少?
分析:(Ⅰ)由PA⊥平面ABC,可得PA⊥BC,又AB为斜边,得BC⊥AC,PA∩AC=A,由直线和平面垂直的判定
定理证得BC⊥平面PAC.
(Ⅱ)由BC⊥平面PAC证得BC⊥AN,又AN⊥PC,可得AN⊥面PBC,从而AN⊥PB.
(Ⅲ)由PB⊥面AMN,可得PB⊥MN,再由AN⊥平面PBC,可得AN⊥MN,故△AMN为直角三角形.用勾股定理
求出AN的值,根据S△AMN=
AN•MN=4
,求得它的最大值.
定理证得BC⊥平面PAC.
(Ⅱ)由BC⊥平面PAC证得BC⊥AN,又AN⊥PC,可得AN⊥面PBC,从而AN⊥PB.
(Ⅲ)由PB⊥面AMN,可得PB⊥MN,再由AN⊥平面PBC,可得AN⊥MN,故△AMN为直角三角形.用勾股定理
求出AN的值,根据S△AMN=
| 1 |
| 2 |
-(tan2θ-
|
解答:解:(Ⅰ)证明:∵PA⊥平面ABC,BC?平面ABC.
∴PA⊥BC,又AB为斜边,∴BC⊥AC,PA∩AC=A,∴BC⊥平面PAC.(4分)
(Ⅱ)证明:∵BC⊥平面PAC,AN?平面PAC,∴BC⊥AN,又AN⊥PC,且BC∩PC=C,
∴AN⊥面PBC,又PB?平面PBC.∴AN⊥PB.
又∵PB⊥AM,AM∩AN=A,∴PB⊥平面AMN.(9分)
(Ⅲ)解:在Rt△PAB中,PA=AB=4,∴PB=4
,∵AM⊥PB,∴AM=
PB=2
,∴PM=BM=2
.
又∵PB⊥面AMN,MN?平面AMN.∴PB⊥MN.∵MN=PM•tanθ=2
tanθ,
∵AN⊥平面PBC,MN?平面PBC.∴AN⊥MN.
∵AN=
=
=
θ,∴S△AMN=
AN•MN=
•2
•
•2
tanθ=4
.
∴当tan2θ=
,即tanθ=
时,S△AMN有最大值为2,
∴当tanθ=
时,S△AMN面积最大,最大值为2. (16分)
∴PA⊥BC,又AB为斜边,∴BC⊥AC,PA∩AC=A,∴BC⊥平面PAC.(4分)
(Ⅱ)证明:∵BC⊥平面PAC,AN?平面PAC,∴BC⊥AN,又AN⊥PC,且BC∩PC=C,
∴AN⊥面PBC,又PB?平面PBC.∴AN⊥PB.
又∵PB⊥AM,AM∩AN=A,∴PB⊥平面AMN.(9分)
(Ⅲ)解:在Rt△PAB中,PA=AB=4,∴PB=4
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
又∵PB⊥面AMN,MN?平面AMN.∴PB⊥MN.∵MN=PM•tanθ=2
| 2 |
∵AN⊥平面PBC,MN?平面PBC.∴AN⊥MN.
∵AN=
| AM2-MN2 |
(2
|
| 8-8tan2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1-tan2θ |
| 2 |
-(tan2θ-
|
∴当tan2θ=
| 1 |
| 2 |
| ||
| 2 |
∴当tanθ=
| ||
| 2 |
点评:题考查证明线面垂直的方法,直线和平面垂直的判定、性质的应用,求出△AMN的面积并化简,是解题的
难点和关键,属于中档题.
难点和关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
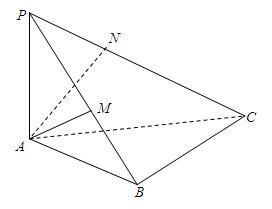 21、如图所示,在斜边为AB的Rt△ABC中,过A作PA⊥平面ABC,AM⊥PB于M,AN⊥PC于N.
21、如图所示,在斜边为AB的Rt△ABC中,过A作PA⊥平面ABC,AM⊥PB于M,AN⊥PC于N.