题目内容
(19)四棱锥P—ABCD的底面是边长为a的正方形,PB⊥面ABCD.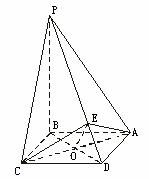
(Ⅰ)若面PAD与面ABCD所成的二面角为60°,求这个四棱锥的体积;
(Ⅱ)证明无论四棱锥的高怎样变化,面PAD与面PCD所成的二面角恒大于90°.
(19)本小题考查线面关系和二面角的概念,以及空间想象能力和逻辑推理能力.
(Ⅰ)解:∵PB⊥面ABCD,

∴BA是PA在面ABCD上的射影.
又DA⊥AB,
∴PA⊥DA,
∴∠PAB是面PAD与面ABCD所成的二面角的平面角,∠PAB=60°.而PB是四棱锥P—ABCD的高,
PB=AB·tan60°=![]() a,
a,
∴V锥=![]() a·a2=
a·a2=![]() a3.
a3.
(Ⅱ)证:不论棱锥的高怎样变化,棱锥侧面PAD与PCD恒为全等三角形.
作AE⊥DP,垂足为E,连结EC,则△ADE≌△CDE,
∴AE=CE,∠CED=90°,故∠CEA是面PAD与面PCD所成的二面角的平面角.
设AC与DB相交于点O,连结EO,则EO⊥AC,
∴![]() a=OA<AE<AD=a.
a=OA<AE<AD=a.
在△AEC中,cosAEC=![]()
=![]() <0.
<0.
所以,面PAD与面PCD所成的二面角恒大于90°.

练习册系列答案
相关题目
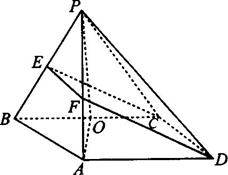
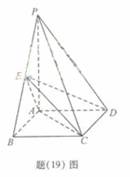 如题(19)图,四棱锥P-ABCD中,底面ABCD为矩形,
如题(19)图,四棱锥P-ABCD中,底面ABCD为矩形, 底面ABCD,PA=AB=
底面ABCD,PA=AB=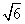 ,点E是棱PB的中点。
,点E是棱PB的中点。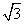 ,求二面角A-EC-D的平面角的余弦值。
,求二面角A-EC-D的平面角的余弦值。