题目内容
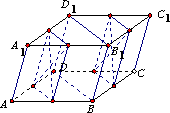
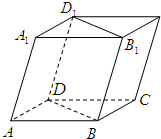如图，过平行六面体ABCD-A1B1C1D1任意两条棱的中点作直线，其中与平面DBB1D1平行的直线共有12
12
条．分析：在平面DBB1D1的一侧，AB、A1B1、A1D1、AD的中点分别为E、F、G、H，根据面面平行的性质可得这四个点的连线有6条都与平面平面DBB1D1平行．同理可得在平面DBB1D1的另一侧也存在6条直线与平面平面DBB1D1平行，故满足条件的直线一共12条．
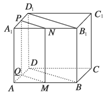
解答：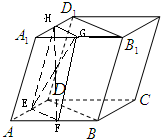
解：设AB、A1B1、A1D1、AD的中点分别为E、F、G、H，连接EF、FG、GH、HE、EG、FH，
∵平面EFGH∥平面DBB1D1，EF、FG、GH、HE、EG、FH都是平面EFGH内的直线
∴EF、FG、GH、HE、EG、FH都与平面平面DBB1D1平行，共6条直线，
同理，在平面DBB1D1的另一侧也存在6条直线与平面平面DBB1D1平行，
因此，满足条件：“与平面DBB1D1平行的直线共有”的直线一共有12条．
故答案为12
解：设AB、A1B1、A1D1、AD的中点分别为E、F、G、H，连接EF、FG、GH、HE、EG、FH，∵平面EFGH∥平面DBB1D1，EF、FG、GH、HE、EG、FH都是平面EFGH内的直线
∴EF、FG、GH、HE、EG、FH都与平面平面DBB1D1平行，共6条直线，
同理，在平面DBB1D1的另一侧也存在6条直线与平面平面DBB1D1平行，
因此，满足条件：“与平面DBB1D1平行的直线共有”的直线一共有12条．
故答案为12
点评：本题给出平行六面体模型，要们找出与已知平面平行的直线的条数，着重考查了平行六面体的性质和空间平行位置关系的判定等知识，属于基础题．
练习册系列答案
相关题目
