题目内容
若函数数f(x)=
x2-
x-
在x=0处的切线l与圆C:x2+y2=1相离,则P(a,b)与圆C的位置关系是( )
| 1 |
| 2 |
| a |
| b |
| 1 |
| b |
分析:利用导数求出函数f(x)=
x2-
x-
在x=0处的切线l的方程,由l与圆C:x2+y2=1相离得到圆心(0,0)到直线l的距离大于圆的半径,整理后得到
<1.从而得到答案.
| 1 |
| 2 |
| a |
| b |
| 1 |
| b |
| a2+b2 |
解答:解:由f(x)=
x2-
x-
,得f′(x)=x-
,
∴f′(0)=-
,又f(0)=-
.
∴函数f(x)=
x2-
x-
在x=0处的切线l为:y+
=-
(x-0),即ax+by+1=0.
∵l与圆C:x2+y2=1相离,
∴圆心(0,0)到直线l的距离大于圆的半径1.
即
>1,
<1.
∴P(a,b)在圆x2+y2=1的内部.
故选:A.
| 1 |
| 2 |
| a |
| b |
| 1 |
| b |
| a |
| b |
∴f′(0)=-
| a |
| b |
| 1 |
| b |
∴函数f(x)=
| 1 |
| 2 |
| a |
| b |
| 1 |
| b |
| 1 |
| b |
| a |
| b |
∵l与圆C:x2+y2=1相离,
∴圆心(0,0)到直线l的距离大于圆的半径1.
即
| 1 | ||
|
| a2+b2 |
∴P(a,b)在圆x2+y2=1的内部.
故选:A.
点评:本题考查了利用导数研究曲线上某点处的切线方程,考查了直线与圆的位置关系,考查了点到直线的距离公式,是中档题.

练习册系列答案
相关题目
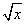 确定数列{an}的反数列为{bn},求{bn}的通项公式;
确定数列{an}的反数列为{bn},求{bn}的通项公式;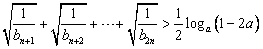 对任意的正整数n恒成立,求实数a的取值范围;
对任意的正整数n恒成立,求实数a的取值范围;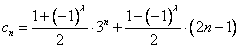 (λ为正整数),若数列{cn}的反数列为{dn},{cn}与{dn}的公共项组成的数列为{tn}, 求数列{tn}前n项和Sn。
(λ为正整数),若数列{cn}的反数列为{dn},{cn}与{dn}的公共项组成的数列为{tn}, 求数列{tn}前n项和Sn。  ;
;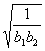 ≥1-2a对任意的正整数n恒成立,求实数a的范围;
≥1-2a对任意的正整数n恒成立,求实数a的范围;