题目内容
函数y=(
)x2-x的单调递减区间是
| 1 |
| 3 |
[
,+∞)
| 1 |
| 2 |
[
,+∞)
;函数y=|lg(x-1)|的增区间是| 1 |
| 2 |
[2,+∞)
[2,+∞)
.分析:根据复合函数的单调性可得,函数t=x2-x 的增区间是[
,+∞),可得函数y=(
)x2-x的单调递减区间是
[
,+∞).结合函数y=|lg(x-1)|的图象,写出它的增区间.
| 1 |
| 2 |
| 1 |
| 3 |
[
| 1 |
| 2 |
解答:解:由复合函数的单调性可得,函数y=(
)x2-x的单调递减区间就是函数t=x2-x 的增区间,
而函数t=x2-x 的增区间是[
,+∞),故函数y=(
)x2-x的单调递减区间是[
,+∞).
把函数y=lgx的图象向右平移1个单位,再把图象位于x轴下方的部分翻折到x轴上方,即得函数y=|lg(x-1)|的图象,如图所示:
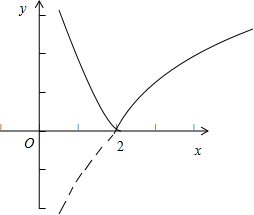
函数y=|lg(x-1)|的增区间是[2,+∞).
故答案为[
,+∞),[2,+∞).
| 1 |
| 3 |
而函数t=x2-x 的增区间是[
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
把函数y=lgx的图象向右平移1个单位,再把图象位于x轴下方的部分翻折到x轴上方,即得函数y=|lg(x-1)|的图象,如图所示:

函数y=|lg(x-1)|的增区间是[2,+∞).
故答案为[
| 1 |
| 2 |
点评:本题主要考查对数函数的单调性和特殊点,指数函数的单调性和特殊点,体现了等价转化、数形结合的数学思想,属于中档题.

练习册系列答案
相关题目