题目内容
在坐标平面 内有一点列An(n=0,1,2,…),其中A(0,0),An(xn,n)(n=1,2,3,…),并且线段AnAn+1所在直线的斜率为2n(n=0,1,2,…).(1)求x1,x2
(2)求出数列{xn}的通项公式xn
(3)设数列{nxn}的前n项和为Sn,求Sn.
【答案】分析:(1)写出A,A1,A2,通过直线的斜率直接求出求x1,x2.
(2)通过直线的斜率关系,推出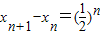 ,利用累加法求出数列{xn}的通项公式xn.
,利用累加法求出数列{xn}的通项公式xn.
(3)写出数列{nxn}的前n项和为Sn,利用错位相减法直接求Sn.
解答:解:(1)A(0,0),A1(x1,1),A2(x2,2)直线AA1的斜率为2=1,
∴x1=1
直线A1A2的斜率为2,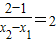 ,
,
∴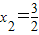
(2)当n≥1时,An(xn,n),An+1(xn+1,n+1),
∴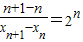 ,
,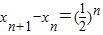
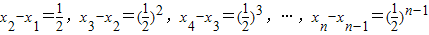
累加得: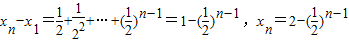 ,
,
检验当n=1时也成立,
∴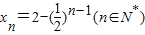
(3)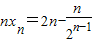 ,令bn=2n,对应的前n项和Tn=n(n+1)令
,令bn=2n,对应的前n项和Tn=n(n+1)令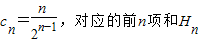
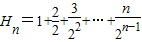

两式相减得: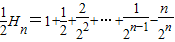
∴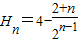
∴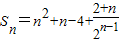
点评:本题是中档题,考查数列项的求法,直线的斜率的应用,考查数列累加法与错位相减法求和的重要方法,常考题型,值得同学们注意和学习.
(2)通过直线的斜率关系,推出
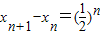 ,利用累加法求出数列{xn}的通项公式xn.
,利用累加法求出数列{xn}的通项公式xn.(3)写出数列{nxn}的前n项和为Sn,利用错位相减法直接求Sn.
解答:解:(1)A(0,0),A1(x1,1),A2(x2,2)直线AA1的斜率为2=1,
∴x1=1
直线A1A2的斜率为2,
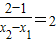 ,
,∴
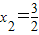
(2)当n≥1时,An(xn,n),An+1(xn+1,n+1),
∴
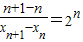 ,
,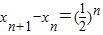
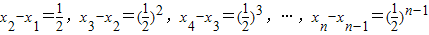
累加得:
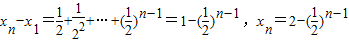 ,
,检验当n=1时也成立,
∴
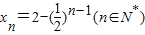
(3)
 ,令bn=2n,对应的前n项和Tn=n(n+1)令
,令bn=2n,对应的前n项和Tn=n(n+1)令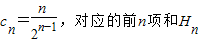
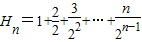

两式相减得:
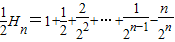
∴
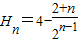
∴
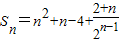
点评:本题是中档题,考查数列项的求法,直线的斜率的应用,考查数列累加法与错位相减法求和的重要方法,常考题型,值得同学们注意和学习.

练习册系列答案
相关题目
 ,其中
,其中 ,
, ,并且线段
,并且线段 所在直线的斜率为
所在直线的斜率为 .
.
 的通项公式
的通项公式
 的前
的前 项和为
项和为 ,求
,求 ,其中
,其中 ,
, ,并且线段
,并且线段 所在直线的斜率为
所在直线的斜率为 .
.
 的通项公式
的通项公式
 的前
的前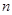 项和为
项和为 ,求
,求