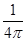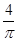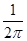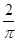题目内容
两根相距3m的木杆上系一根拉直的绳子，并在绳子上挂一彩珠，则彩珠与两端距离都大于1m的概率为( )
A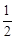． | B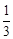． | C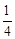． | D． |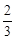
B
解析试题分析：两根相距3m的木杆上系一根拉直的绳子，并在绳子上挂一彩珠，则彩珠与两端距离都大于1m的位置处在中间一米的位置，所以由几何概型概率的计算公式得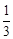，故选B。
考点：本题主要考查几何概型概率的计算。
点评：简单题，几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．
练习册系列答案
相关题目
一件产品要经过2道独立的加工工序，第一道工序的次品率为ａ，第二道工序的次品率为ｂ，则产品的正品率为（ ）：
| A． 1-ａ-ｂ | B．1-ａ·ｂ |
| C．（1-ａ）·（1-ｂ） | D．1-（1-ａ）·（1-ｂ） |
同时掷两枚骰子,所得点数之和为5的概率为 （ ）
A． | B． | C． | D． |
把一枚硬币连续抛掷两次，事件
“第一次出现正面”,事件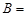
“第二次出现正面”，则
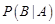等于（ ）
A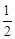． | B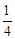． | C． | D． |
记
分别是投掷两次骰子所得的数字，则方程
有两个不同实根的概率为（ ）
A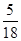． | B． | C． | D． |
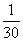
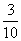
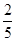
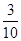
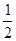cm的正方形孔,若你随机向铜钱上滴一滴油,则油(油滴的大小忽略不计)正好落入孔中的概率是（ ）
