题目内容
已知点P在曲线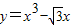 上移动,在点P处的切线倾斜角为α,则α的取值范围是( )
上移动,在点P处的切线倾斜角为α,则α的取值范围是( )A.
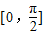
B.
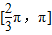
C.
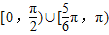
D.
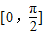 ∪
∪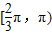
【答案】分析:根据导数的几何意义可知切线的斜率即为该点处的导数,再根据导数的取值范围求出斜率的范围,最后再根据斜率与倾斜角之间的关系k=tanα,求出α的范围即可.
解答:解:∵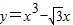 ,
,
∴y′=3x2-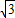 ,
,
∴tanα=3x2-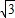 ,
,
∴tanα∈[-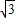 ,+∞).
,+∞).
当tanα∈[0,+∞)时,α∈[0,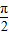 );
);
当tanα∈[-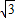 ,0)时,α∈[
,0)时,α∈[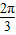 ,π).
,π).
∴α∈[0,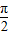 )∪[
)∪[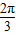 ,π).
,π).
故选D.
点评:考查学生会利用导数求曲线上过某点切线方程的斜率,会利用切线的斜率与倾斜角之间的关系k=tanα进行求解.
解答:解:∵
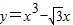 ,
,∴y′=3x2-
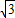 ,
,∴tanα=3x2-
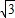 ,
,∴tanα∈[-
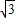 ,+∞).
,+∞).当tanα∈[0,+∞)时,α∈[0,
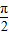 );
);当tanα∈[-
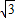 ,0)时,α∈[
,0)时,α∈[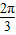 ,π).
,π).∴α∈[0,
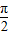 )∪[
)∪[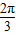 ,π).
,π).故选D.
点评:考查学生会利用导数求曲线上过某点切线方程的斜率,会利用切线的斜率与倾斜角之间的关系k=tanα进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 上移动,在点P处的切线倾斜角为
上移动,在点P处的切线倾斜角为  ,则
,则  的 取值范围是
的 取值范围是 B.
B. C.
C. D.
D. 
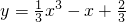 上移动,若经过点P的曲线的切线的倾斜角为α,则α的取值范围是________.
上移动,若经过点P的曲线的切线的倾斜角为α,则α的取值范围是________.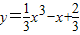 上移动,若经过点P的曲线的切线的倾斜角为α,则α的取值范围是 .
上移动,若经过点P的曲线的切线的倾斜角为α,则α的取值范围是 .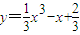 上移动,若经过点P的曲线的切线的倾斜角为α,则α的取值范围是 .
上移动,若经过点P的曲线的切线的倾斜角为α,则α的取值范围是 .