题目内容
已知函数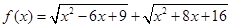 .
.
(Ⅰ)求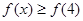 的解集;
的解集;
(Ⅱ)设函数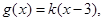
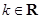 ,若
,若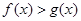 对任意的
对任意的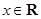 都成立,求
都成立,求 的取值范围.
的取值范围.
(Ⅰ)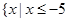 或
或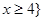 (Ⅱ)
(Ⅱ)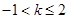
解析试题分析:(Ⅰ)先利用根式的性质将函数 的解析式化为含绝对的函数,在将
的解析式化为含绝对的函数,在将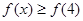 具体化为
具体化为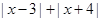
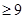 ,利用零点分析法化为不等式组,通过解不等式组解出
,利用零点分析法化为不等式组,通过解不等式组解出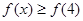 的解集;(Ⅱ)利用零点分析法,通过分讨论将
的解集;(Ⅱ)利用零点分析法,通过分讨论将 的解析式化为分段函数,作出函数
的解析式化为分段函数,作出函数 的图像,由函数
的图像,由函数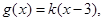
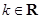 知,函数
知,函数 图像是恒过(3,0),斜率为
图像是恒过(3,0),斜率为 的直线,由
的直线,由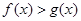 对任意的
对任意的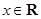 都成立知,函数
都成立知,函数 的图像恒在函数
的图像恒在函数 的上方,作出函数
的上方,作出函数 的图像,观察
的图像,观察 满足的条件,求出
满足的条件,求出 的取值范围.
的取值范围.
试题解析:(Ⅰ)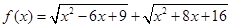
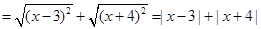
∴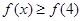 即
即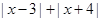
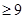
∴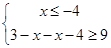 ① 或
① 或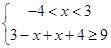 ② 或
② 或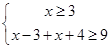 ③
③
解得不等式①: ;②:无解 ③:
;②:无解 ③: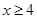
所以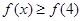 的解集为
的解集为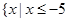 或
或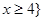 . 5分
. 5分
(Ⅱ)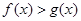 即
即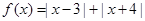 的图象恒在
的图象恒在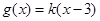 图象的上方
图象的上方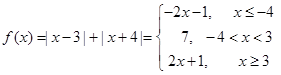
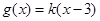 图象为恒过定点
图象为恒过定点
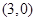 ,且斜率
,且斜率 变化的一条直线作函数
变化的一条直线作函数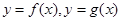 图象如图,
图象如图,
其中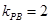 ,
,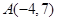 ,∴
,∴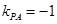
由图可知,要使得 的图象恒在
的图象恒在 图象的上方
图象的上方
∴实数 的取值范围为
的取值范围为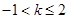 . 10分
. 10分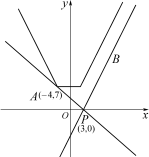
考点:根式性质,含绝对不等式解法,分段函数,数形结合思想,分类整合思想

练习册系列答案
相关题目
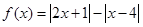
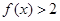 ;
; 的最小值.
的最小值.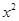 -(
-(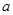 +
+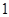 )
)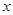 +
+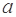 ∈R).
∈R).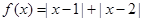
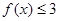 的解集;
的解集;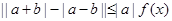 (
(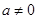 ,
,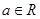 ,
,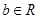 )恒成立,求实数
)恒成立,求实数 的范围.
的范围.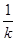 },求k的值;
},求k的值; 的解集为 .
的解集为 .