题目内容
从{1,2,3,4,5}中随机选取一个数为a,从{1,2,3}中随机选取一个数为b,则b>a的概率是( )
A.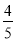 B.
B. C.
C.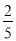 D.
D.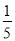
练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
题目内容
从{1,2,3,4,5}中随机选取一个数为a,从{1,2,3}中随机选取一个数为b,则b>a的概率是( )
A.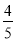 B.
B. C.
C.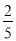 D.
D.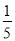
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案