题目内容
已知圆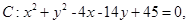 及点
及点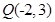 .
.
(1) 在圆上,求线段
在圆上,求线段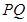 的长及直线
的长及直线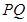 的斜率;
的斜率;
(2)若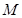 为圆
为圆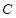 上任一点,求
上任一点,求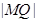 的最大值和最小值;
的最大值和最小值;
(3)若实数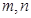 满足
满足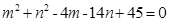 ,求
,求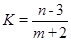 的最大值和最小值.
的最大值和最小值.
【答案】
(1)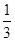 (2)最小值
(2)最小值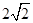 ,最大值
,最大值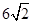 (3)
(3)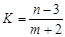 的最大值为
的最大值为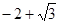 ,最小值为
,最小值为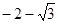
【解析】
试题分析:(1)将P(a,a+1)代入C:x2+y2-4x-14y+45=0,中得a=4,所以p(4,5),|PQ|=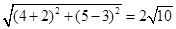 ,kpQ=
,kpQ=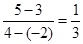
(2)将圆C:x2+y2-4x-14y+45=0,转化为标准形式(x-2)2+(y-7)2=(2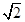 )2圆心C(2,7)|QC|-R≤|MQ|≤|QC|+R,因为|QC|=4
)2圆心C(2,7)|QC|-R≤|MQ|≤|QC|+R,因为|QC|=4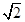 ,所以2
,所以2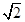 ≤|MQ|≤6
≤|MQ|≤6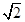 ,所以|MQ|最小值为2
,所以|MQ|最小值为2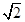 ,最大值为6
,最大值为6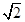
(3)根据题意,实数m,n满足m2+n2-4m-14n+45=0,即满足(m-2)2+(n-7)2=(2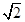 )2,则(m,n)对应的点在以(2,7)为圆心,半径为2
)2,则(m,n)对应的点在以(2,7)为圆心,半径为2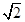 的圆上,分析可得K=
的圆上,分析可得K=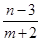 表示该圆上的任意一点与Q(-2,3,)相连所得直线的斜率,设该直线斜率为k,则其方程为y-3=k(x+2),又由d=
表示该圆上的任意一点与Q(-2,3,)相连所得直线的斜率,设该直线斜率为k,则其方程为y-3=k(x+2),又由d=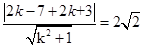 ,解得k=2±
,解得k=2±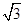 即2-
即2-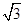 ≤K≤2+
≤K≤2+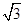 所以
所以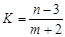 的最大值为
的最大值为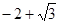 ,最小值为
,最小值为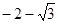
考点:本题考查了点、线、圆的关系
点评:此类问题考查了直线与圆的方程的综合.考查了学生数形结合的思想,函数的思想,转化和化归的思想的运用.

练习册系列答案
相关题目
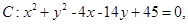 及点
及点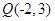 .
.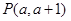 在圆上,求线段
在圆上,求线段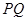 的长及直线
的长及直线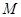 为圆
为圆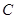 上任一点,求
上任一点,求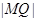 的最大值和最小值;
的最大值和最小值;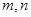 满足
满足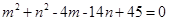 ,求
,求 的最大值和最小值.
的最大值和最小值.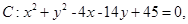 及点
及点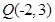 .
.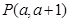 在圆上,求线段
在圆上,求线段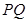 的长及直线
的长及直线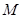 为圆
为圆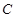 上任一点,求
上任一点,求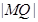 的最大值和最小值;
的最大值和最小值;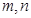 满足
满足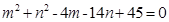 ,求
,求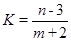 的最大值和最小值.
的最大值和最小值. 及点
及点 .
. 在圆上,求线段
在圆上,求线段 的长及直线
的长及直线 为圆
为圆 上任一点,求
上任一点,求 的最大值和最小值;
的最大值和最小值; 满足
满足 ,求
,求 的最大值和最小值.
的最大值和最小值.