Question

如果关于实数x的方程ax2+

1

x

=3x的所有解中，仅有一个正数解，那么实数a的取值范围为（　　）

A．{a|-2≤a≤2}

B．{a|a≤0或a=2}

C．{a|a≥2或a＜-2}

D．{a|a≥0或a=-2}

Answer 1

分析：原条件?a=

3

x

-

1

x3

有且仅有一个正实数解，令

1

x

=t(t≠0)，t的符号与x的符号一致，则a=-t³+3t有且仅有一个正实数解，然后通过导数研究函数的单调性和极值，画出函数图象，结合图象可求出a的取值范围．

解答：解：关于实数x的方程ax2+

1

x

=3x的所有解中，仅有一个正数解?a=

3

x

-

1

x3

有且仅有一个正实数解．
令

1

x

=t(t≠0)，t的符号与x的符号一致，则a=-t³+3t有且仅有一个正实数解，
令f（t）=-t³+3t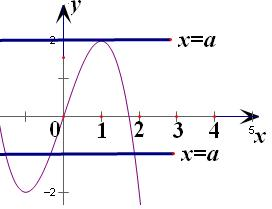（t≠0），
f′（t）=-3t²+3，由f′（t）=0得t=1或t=-1．
又t∈（-1，1）时，f′（t）＞0；t∈（-∞，-1），（1，+∞）时，
f′（t）＜0．所以[f（t）]_极大值=f（1）=2．
又t→-∞，f（t）→+∞；t→+∞，f（t）→-∞．
结合三次函数图象即可．
综上所述，实数a的取值范围为（-∞，0]∪{2}．
故选B．

点评：本题主要考查了根的存在性及根的个数判断，以及三次函数的性质，同时考查了数形结合与函数方程的思想，属于中档题．