题目内容
下列命题:①若区间D内任意实数x都有f(x+1)>f(x),则y=f(x)在D上是增函数;②y=-
在定义域内是增函数;③函数f(x)=
图象关于原点对称;④如果关于实数x的方程ax2+
=3x的所有解中,正数解仅有一个,那么实数a的取值范围是a≤0; 其中正确的序号是
| 1 |
| x |
| ||
| |x+1|-1 |
| 1 |
| x |
③
③
.分析:根据函数单调性的定义,我们可以判断①的真假;根据反比例函数的图象和性质,我们可以判断②的真假;根据函数奇偶性的定义及图象特征,可以判断③的真假;根据方程根与函数零点的关系,我们判断出关于实数x的方程ax2+
=3x的所有解中,正数解仅有一个时,参数a的取值范围,即可判断④的真假,进而得到答案.
| 1 |
| x |
解答:解:①若区间D内任意实数x都有f(x+1)>f(x),但不一定满足增函数的定义,则y=f(x)在D上是增函数错误;
②y=-
在(-∞,0)和(0,+∞)上均为增函数,但在其定义域内不是增函数,故②错误;
③∵函数f(x)=
为奇函数,∴函数f(x)=
的图象关于原点对称,故③正确;
④将方程ax2+
=3x改写为
=3x-ax2,令 y1=
,y2=3x-ax2.
“关于实数x的方ax2+
=3x的所有解中,仅有一个正数解”等价于“双曲线y1=
与y2=3x-ax2的图象在y轴右侧只有一个交点”.
双曲线y1=
在第一、三象限内.
当a>0时,抛物线y2=3x-ax2的开口向下且过原点(0,0)及x轴正半轴上的点 (3a,0),研究知,当a<2时,双曲线y1=
与抛物线y2=3x-ax2在第一象限内有两个交点,当a>2时,两曲线在第一象限无交点,当a=2进,两曲线仅有一个交点,故a=2符合题意.
当a=0时,y2=3x-ax2为直线,此时,双曲线y1=
与直线y2=3x在第一象限内只有一个交点,故a=0符合题意.
当a<0时,抛物线y2=3x-ax2的开口向上且过原点(0,0)及x轴负半轴上的点 (3a,0),此时,双曲线 y1=
与抛物线y2=3x-ax2在第一象限内仅有一个交点,故a<0符合题意.
综上所述,实数a的取值范围为(-∞,0]∪{2}.,故④错误;
故答案为:③
②y=-
| 1 |
| x |
③∵函数f(x)=
| ||
| |x+1|-1 |
| ||
| |x+1|-1 |
④将方程ax2+
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
“关于实数x的方ax2+
| 1 |
| x |
| 1 |
| x |
双曲线y1=
| 1 |
| x |
当a>0时,抛物线y2=3x-ax2的开口向下且过原点(0,0)及x轴正半轴上的点 (3a,0),研究知,当a<2时,双曲线y1=
| 1 |
| x |
当a=0时,y2=3x-ax2为直线,此时,双曲线y1=
| 1 |
| x |
当a<0时,抛物线y2=3x-ax2的开口向上且过原点(0,0)及x轴负半轴上的点 (3a,0),此时,双曲线 y1=
| 1 |
| x |
综上所述,实数a的取值范围为(-∞,0]∪{2}.,故④错误;
故答案为:③
点评:本题考查的知识点是函数奇偶性的判断,方根根的个数及判断,对称图形,函数单调性的定义及判断,熟练掌握函数图象及性质,是解答本题的关键.

练习册系列答案
相关题目
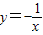 在定义域内是增函数;
在定义域内是增函数;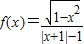 图象关于原点对称;
图象关于原点对称; 在定义域内是增函数;③函数
在定义域内是增函数;③函数 图象关于原点对称;④既是奇函数又是偶函数的函数一定是
图象关于原点对称;④既是奇函数又是偶函数的函数一定是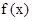 =0
=0  ; ⑤函数y=f(x+2)图象与函数y=f(2-x)图象关于直线x=2对称;其中正确命题的个数为:(
)
; ⑤函数y=f(x+2)图象与函数y=f(2-x)图象关于直线x=2对称;其中正确命题的个数为:(
)