题目内容
设四点A、B、C、D均在双曲线x2-y2=1的右支上．（1）若
| AB |
| CD |
| OA |
| OB |
| OC |
| OD |
（2）若|AB|=2，P是线段AB的中点，过点P分别作该双曲线的两条渐近线的垂线，垂足为M、N，求四边形OMPN的面积的最大值．
分析：（1）据两向量共线的充要条件得两向量共线，据两线平行斜率相等，设出直线方程与曲线方程联立，利用韦达定理代入得证．
（2）利用弦长公式得到斜率与截距的关系，据四边形为两个三角形面积的和表示出面积，转化为求函数的最大值．
（2）利用弦长公式得到斜率与截距的关系，据四边形为两个三角形面积的和表示出面积，转化为求函数的最大值．
解答：解：（1）∵
=λ
，∴
∥
①直线AB的斜率不存在时，
设方程为x=m（|m|＞1），
设A（m，y1），则B（m，-y1）且m2-y12=1
∴
•
=m2-y12=1同理
•
=1
∴
•
=
•
②直线AB斜率存在时，设方程为y=kx+b
与x2-y2=1联立得（1-k2）x2-2kbx-b2-1=0
设A（x1，y1）B（x2，y2）则x1+x2=
，x1x2=
则
•
=x1x2+y1y2=x1x2+（kx1+b）（kx2+b）=（1+k2）x1x2+kb（x1+x2）+b2=
∵AB∥CD∴直线CD与直线AB斜率相等，同理
•
=
∴
•
=
•
综上，
•
=
•
（2）AB斜率存在时，4=|AB|2=（1+k2）[（x1+x2）2-4x1x2]
由（1）②得b2=
∵x1•x2＞0∴k2＞1，设P（x0，y0），则x0=
(x1+x2)=
y0=kx0+b=
∴S=
•
=
•
=1-
∵k2＞1∴
＜S＜1；AB斜率不存在时，易得S=1
综上，四边形OMPN面积的最大值为1．
| AB |
| CD |
| AB |
| CD |
①直线AB的斜率不存在时，
设方程为x=m（|m|＞1），
设A（m，y1），则B（m，-y1）且m2-y12=1
∴
| OA |
| OB |
| OC |
| OD |
∴
| OA |
| OB |
| OC |
| OD |
②直线AB斜率存在时，设方程为y=kx+b
与x2-y2=1联立得（1-k2）x2-2kbx-b2-1=0
设A（x1，y1）B（x2，y2）则x1+x2=
| 2kb |
| 1-k2 |
| b2+1 |
| k2-1 |
则
| OA |
| OB |
| k2+1 |
| k2-1 |
∵AB∥CD∴直线CD与直线AB斜率相等，同理
| OC |
| OD |
| k2+1 |
| k2-1 |
∴
| OA |
| OB |
| OC |
| OD |
| OA |
| OB |
| OC |
| OD |
（2）AB斜率存在时，4=|AB|2=（1+k2）[（x1+x2）2-4x1x2]
由（1）②得b2=
| 2k2(k2-1) |
| 1+k2 |
| 1 |
| 2 |
| kb |
| 1-k2 |
| b |
| 1-k2 |
| |x0-y0| | ||
|
| |x0+y0| | ||
|
| 1 |
| 2 |
| b2 |
| k2-1 |
| 1 |
| 1+k2 |
∵k2＞1∴
| 1 |
| 2 |
综上，四边形OMPN面积的最大值为1．
点评：本题考查向量共线的充要条件；解决直线与圆锥曲线问题的方法；直线与圆锥曲线相交截的得的弦长公式等．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
=
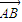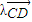（实数λ≠0），证明：
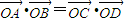（O是坐标原点）；
=
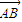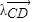（实数λ≠0），证明：
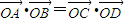（O是坐标原点）；