题目内容
在△ABC中,AB⊥AC,AB=6,AC=4,D为AC的中点,点E在边AB上,且3AE=AB,BD与CE交于点G,则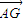 •
•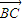 = .
= .
【答案】分析:先DH∥AB交CE于H,利用三角形的相似得出BG=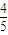 BD,从而可表示出
BD,从而可表示出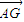 ,进而可得
,进而可得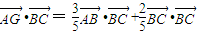 ,利用向量的数量积公式即可求得.
,利用向量的数量积公式即可求得.
解答: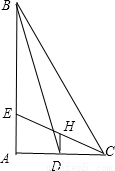 解:作DH∥AB交CE于H,则DH为△AEC的中位线
解:作DH∥AB交CE于H,则DH为△AEC的中位线
∵3AE=AB,AB=6,
∴AE=2,
∴DH= AE=1,
AE=1,
∵DH∥AB,∴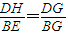 ,所以BG=
,所以BG=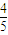 BD
BD
∵D为AC的中点,∴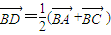
∴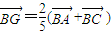
∴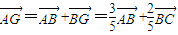
∴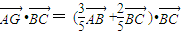 =
=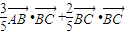
∵AB⊥AC,AB=6,AC=4
∴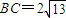 ,
,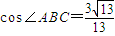
∴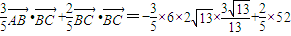 =
=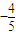
∴
故答案为: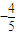
点评:本题以三角形为载体,考查向量的数量积运算,解题的关键是根据比例关系得出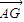 ,从而可得
,从而可得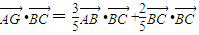 .
.
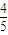 BD,从而可表示出
BD,从而可表示出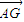 ,进而可得
,进而可得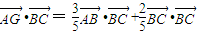 ,利用向量的数量积公式即可求得.
,利用向量的数量积公式即可求得.解答:
 解:作DH∥AB交CE于H,则DH为△AEC的中位线
解:作DH∥AB交CE于H,则DH为△AEC的中位线∵3AE=AB,AB=6,
∴AE=2,
∴DH=
 AE=1,
AE=1,∵DH∥AB,∴
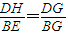 ,所以BG=
,所以BG=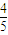 BD
BD∵D为AC的中点,∴
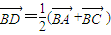
∴
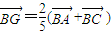
∴
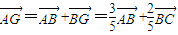
∴
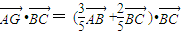 =
=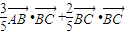
∵AB⊥AC,AB=6,AC=4
∴
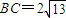 ,
,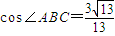
∴
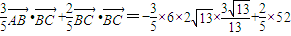 =
=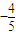
∴

故答案为:
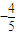
点评:本题以三角形为载体,考查向量的数量积运算,解题的关键是根据比例关系得出
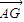 ,从而可得
,从而可得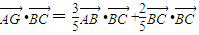 .
. 
练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目