题目内容
 如图所示,平面α∥平面β,点A∈α,C∈α,点B∈β,D∈β,点E,F分别在线段AB,CD上,AB,CD所在直线异面,且AE:EB=CF:FD
如图所示,平面α∥平面β,点A∈α,C∈α,点B∈β,D∈β,点E,F分别在线段AB,CD上,AB,CD所在直线异面,且AE:EB=CF:FD(Ⅰ)求证:EF∥β;
(Ⅱ)若E,F分别是AB,CD的中点,AC=4,BD=6,且AC,BD所成的角为60°,求EF的长.
分析:(Ⅰ)直接连接AD,作EG∥BD交AD于点G,连接FG;结合AE:EB=CF:FD可得EG∥β,FG∥α;进而得到平面EFG∥β即可证得结论;
(Ⅱ)结合第一问中的结论和AC,BD所成的角为60°可以得到EG=
BD=3,FG=
AC=2以及∠EGF=120°或60°;最后利用余弦定理即可求出结论.
(Ⅱ)结合第一问中的结论和AC,BD所成的角为60°可以得到EG=
| 1 |
| 2 |
| 1 |
| 2 |
解答: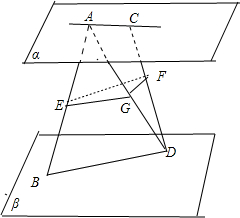 (Ⅰ)证明:连接AD,作EG∥BD交AD于点G,连接FG,
(Ⅰ)证明:连接AD,作EG∥BD交AD于点G,连接FG,
因为AE:EB=CF:FD
∴EG∥BD,FG∥AC,
则EG∥β,FG∥α,
∵α∥β
∴FG∥β;
又因为;EG∩FG=G.
∴平面EFG∥β
而EF?平面EFG;
∴EF∥β
(Ⅱ)解:∵EG∥BD,FG∥AC且E,F分别是AB,CD的中点,AC=4,BD=6;
∴EG=
BD=3,FG=
AC=2
∵AC,BD所成的角为60°,
∴∠EGF=120°或60°
∴EF=
=
=
;
或EF=
=
即EF=
或
.
 (Ⅰ)证明:连接AD,作EG∥BD交AD于点G,连接FG,
(Ⅰ)证明:连接AD,作EG∥BD交AD于点G,连接FG,因为AE:EB=CF:FD
∴EG∥BD,FG∥AC,
则EG∥β,FG∥α,
∵α∥β
∴FG∥β;
又因为;EG∩FG=G.
∴平面EFG∥β
而EF?平面EFG;
∴EF∥β
(Ⅱ)解:∵EG∥BD,FG∥AC且E,F分别是AB,CD的中点,AC=4,BD=6;
∴EG=
| 1 |
| 2 |
| 1 |
| 2 |
∵AC,BD所成的角为60°,
∴∠EGF=120°或60°
∴EF=
| EG 2+FG 2-2EG•FGcos∠EGF |
| 22+32-2×2×3cos∠120° |
| 19 |
或EF=
| 22+32-2×2×3×cos∠60° |
| 7 |
即EF=
| 19 |
| 7 |
点评:本题主要考查空间中线段距离的计算以及线面平行的判定.在求线段长度问题是,一般是放在三角形中,借助于正弦定理或余弦定理求解.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目

 如图所示,一隧道内设双行线公路,其截面由长方形的三条边和抛物线的一段构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米.
如图所示,一隧道内设双行线公路,其截面由长方形的三条边和抛物线的一段构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米.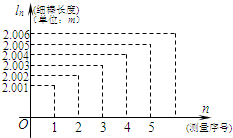 为了测试某种金属的热膨胀性能,将这种金属的一根细棒加热,从100℃开始第一次量细棒的长度,以后每升高40℃量一次,把依次量得的数据所成的数列{ln}用图象表示如图所示.若该金属在20℃~500℃之间,热膨胀性能与温度成一次函数关系,试根据图象回答下列问题:
为了测试某种金属的热膨胀性能,将这种金属的一根细棒加热,从100℃开始第一次量细棒的长度,以后每升高40℃量一次,把依次量得的数据所成的数列{ln}用图象表示如图所示.若该金属在20℃~500℃之间,热膨胀性能与温度成一次函数关系,试根据图象回答下列问题: (2012•自贡三模)如图所示,己知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,P点在A1B1上,且满足
(2012•自贡三模)如图所示,己知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,P点在A1B1上,且满足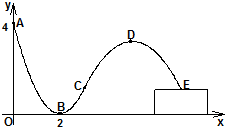 轮滑是穿着带滚轮的特制鞋在坚硬的场地上滑行的运动.如图,助跑道ABC是一段抛物线,某轮滑运动员通过助跑道获取速度后飞离跑道然后落到离地面高为1米的平台上E处,飞行的轨迹是一段抛物线CDE(抛物线CDE与抛物线ABC在同一平面内),D为这段抛物线的最高点.现在运动员的滑行轨迹所在平面上建立如图所示的直角坐标系,x轴在地面上,助跑道一端点A(0,4),另一端点C(3,1),点B(2,0),单位:米.
轮滑是穿着带滚轮的特制鞋在坚硬的场地上滑行的运动.如图,助跑道ABC是一段抛物线,某轮滑运动员通过助跑道获取速度后飞离跑道然后落到离地面高为1米的平台上E处,飞行的轨迹是一段抛物线CDE(抛物线CDE与抛物线ABC在同一平面内),D为这段抛物线的最高点.现在运动员的滑行轨迹所在平面上建立如图所示的直角坐标系,x轴在地面上,助跑道一端点A(0,4),另一端点C(3,1),点B(2,0),单位:米.