题目内容
函数f(x)=x3+sinx+1(x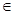
R)，若f(a)=2,则f(－a)的值为 ( )
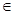R)，若f(a)=2,则f(－a)的值为 ( )| A．3 | B．0 | C．－1 | D．－2 |
B
解：因为f(x)=x3+sinx+1(x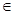R)，故g(x)="f(x)-1=" x3+sinx为奇函数，则
g(a)+g(-a)=0,即f(a)+f(－a)=2，因为f(a)=2，所以f(－a)=0，故选B
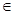R)，故g(x)="f(x)-1=" x3+sinx为奇函数，则g(a)+g(-a)=0,即f(a)+f(－a)=2，因为f(a)=2，所以f(－a)=0，故选B
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
，则下列结论正确的是：
的图象关于点
中心对称 
上单调递增
个单位后关于y轴对称
的顶点在坐标原点，始边与x轴的非负半轴重合，终边经过点P
．
的值； 
图象的对称中心为
，求
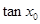的值．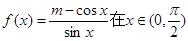
单调递增，则实数
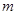的取值范围为（ ）
，
，
⊥
； （2）
，求
的值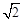
sin2x上所有的点
个单位
个单位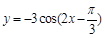 
的初相是 
的最小正周期是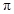
，那么正数
（ ）
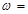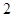
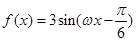
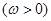和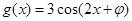
的图象完全相同，若
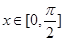，则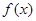
的取值范围是___▲___.