题目内容
已知函数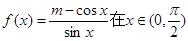 单调递增,则实数
单调递增,则实数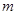 的取值范围为( )
的取值范围为( )
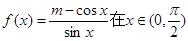 单调递增,则实数
单调递增,则实数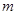 的取值范围为( )
的取值范围为( )A. | B. | C. | D. |
分析:由题意可求得,f′(x)=
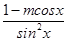 ,利用f(x)=
,利用f(x)= 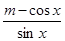 在(0,
在(0, 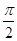 )单调递增,可得mcosx≤1,x∈(0,
)单调递增,可得mcosx≤1,x∈(0,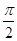 ),从而可求得实数m的取值范围.
),从而可求得实数m的取值范围.解:由题意得:f′(x)=
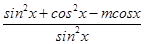 =
=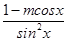 ,
,∵f(x)=
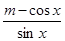 在(0,
在(0,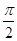 )单调递增,
)单调递增,∴f′(x)≥0,x∈(0,
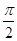 ),
),∴1-mcosx≥0,x∈(0,
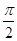 ),即mcosx≤1,
),即mcosx≤1,∵x∈(0,
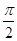 ),
),∴cosx>0,
∴m≤
 ,x∈(0,
,x∈(0,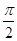 ),
),∴m≤1.
故选B.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
 个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是( )
个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是( ) )
) x-
x- )
) ,
, .
. 是函数
是函数 图象的一条对称轴,求
图象的一条对称轴,求 的值;
的值; 的单调递增区间.
的单调递增区间.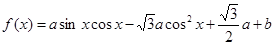
 〉0时,写出函数的单调递减区间;
〉0时,写出函数的单调递减区间;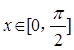 ,
,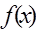 的最小值是
的最小值是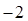 ,最大值是
,最大值是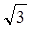 ,求实数
,求实数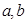 的值.
的值. ),(
),(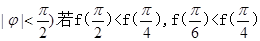 ,则
,则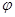 的取值范围为 .
的取值范围为 .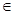 R),若f(a)=2,则f(-a)的值为 ( )
R),若f(a)=2,则f(-a)的值为 ( )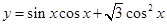 的图象的一个对称中心是
的图象的一个对称中心是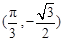
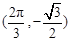
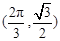
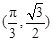
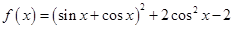 .
.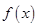 的最小正周期;
的最小正周期;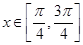 时,求函数
时,求函数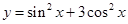 的最小正周期为_____.
的最小正周期为_____.