题目内容
从装有2只红球,2只白球和1只黑球的袋中逐一取球,已知每只球被抽取的可能性相同.
(Ⅰ)若抽取后又放回,抽取3次,求恰好抽到2次为红球的概率;
(Ⅱ)若抽取后不放回,设抽完红球所需的次数为s4,求s4的分布列及期望.
(Ⅰ)若抽取后又放回,抽取3次,求恰好抽到2次为红球的概率;
(Ⅱ)若抽取后不放回,设抽完红球所需的次数为s4,求s4的分布列及期望.
分析:(Ⅰ)抽取一次取到红球的概率为
,由此能求出抽取3次恰好有两次取到红球的概率.
(Ⅱ)由题设知s4的可能取值为2,3,4,5,分别求出P(s4=2),P(s4=3),P(s4=4),P(s4=5),由此能求出s4的分布列和E(s4).
| 2 |
| 5 |
(Ⅱ)由题设知s4的可能取值为2,3,4,5,分别求出P(s4=2),P(s4=3),P(s4=4),P(s4=5),由此能求出s4的分布列和E(s4).
解答:解:(Ⅰ)抽取一次取到红球的概率为
,
∴抽取3次恰好有两次取到红球的概率为:
P=
(
)2(
)=
.
(Ⅱ)由题设知s4的可能取值为2,3,4,5,
P(s4=2)=
=
,
P(s4=3)=
=
,
P(s4=4)=
=
,
P(s4=5)=
=
,
∴s4的分布列为:
∴E(s4)=2×
+3×
+4×
+5×
=4.
| 2 |
| 5 |
∴抽取3次恰好有两次取到红球的概率为:
P=
| C | 2 3 |
| 2 |
| 5 |
| 3 |
| 5 |
| 36 |
| 125 |
(Ⅱ)由题设知s4的可能取值为2,3,4,5,
P(s4=2)=
| ||
|
| 1 |
| 10 |
P(s4=3)=
| ||||||
|
| 1 |
| 5 |
P(s4=4)=
| ||||||
|
| 3 |
| 10 |
P(s4=5)=
| ||||||
|
| 2 |
| 5 |
∴s4的分布列为:
| s4 | 2 | 3 | 4 | 5 | ||||||||
| P |
|
|
|
|
| 1 |
| 10 |
| 1 |
| 5 |
| 3 |
| 10 |
| 2 |
| 5 |
点评:本题考查离散型随机变量的分布列和数学期望,是中档题,在历年高考中都是必考题型.解题时要认真审题,仔细解答,注意排列组合和概率知识的灵活运用.

练习册系列答案
相关题目
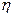 的数学期望
的数学期望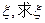 的分布列及期望。
的分布列及期望。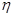 的数学期望
的数学期望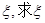 的分布列及期望。
的分布列及期望。