题目内容
从装有2只红球,2只白球和1只黑球的袋中逐一取球,已知每只球被抽取的可能性相同.(1)若抽取后又放回,抽3次,分别求恰2次为红球的概率及抽全三种颜色球的概率;
(2)若抽取后不放回,抽完红球所需次数为ξ,求ξ的分布列及期望.
分析:(1)抽取后又放回,每次取球可看作独立重复试验,利用独立重复试验求解即可.
(2)抽取后不放回,ξ所有可能的取值为2,3,4,5,分别求出其概率即可.
(2)抽取后不放回,ξ所有可能的取值为2,3,4,5,分别求出其概率即可.
解答:解:(1)抽1次得到红球的概率为
,得白球的概率为
,得黑球的概率为
.
所以恰2次为红色球的概率为P1=
(
)2
=
抽全三种颜色的概率P2=
×
×
•
=
(2)ξ的分布列为

即

∴Eξ=4
| 2 |
| 5 |
| 2 |
| 5 |
| 1 |
| 5 |
所以恰2次为红色球的概率为P1=
| C | 2 3 |
| 2 |
| 5 |
| 3 |
| 5 |
| 36 |
| 125 |
抽全三种颜色的概率P2=
| 2 |
| 5 |
| 2 |
| 5 |
| 1 |
| 5 |
| A | 3 3 |
| 24 |
| 125 |
(2)ξ的分布列为

即

∴Eξ=4
点评:本题考查排列组和、离散型随机变量的分布列问题,同时考查利用概率分析、解决问题的能力.在取球试验中注意是否有放回.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
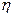 的数学期望
的数学期望 的分布列及期望。
的分布列及期望。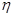 的数学期望
的数学期望 的分布列及期望。
的分布列及期望。