题目内容
 空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:| PM2.5 日均浓度 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 | >250 |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类型 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
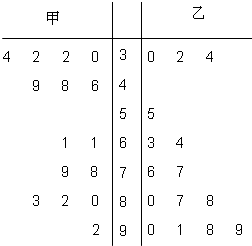
(Ⅰ)根据你所学的统计知识估计甲、乙两城市15天内哪个城市空气质量总体较好?(注:不需说明理由)
(Ⅱ)在15天内任取1天,估计甲、乙两城市空气质量类别均为优或良的概率;
(Ⅲ)在乙城市15个监测数据中任取2个,设X为空气质量类别为优或良的天数,求X的分布列及数学期望.
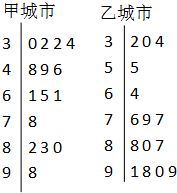
【答案】分析:(I)由茎叶图可知:甲城市空气质量一级和二级共有10天,而乙城市空气质量一级和二级只有5天,因此甲城市空气质量总体较好.
(II)由(I)的分析及相互独立事件的概率计算公式即可得出;
(III)利用超几何分布即可得到分布列,再利用数学期望的计算公式即可得出.
解答:解:(Ⅰ)甲城市空气质量总体较好.
(Ⅱ)甲城市在15天内空气质量类别为优或良的共有10天,任取1天,空气质量类别为优或良的概率为 ,
,
乙城市在15天内空气质量类别为优或良的共有5天,任取1天,空气质量类别为优或良的概率为 ,
,
在15天内任取1天,估计甲、乙两城市空气质量类别均为优或良的概率为 .
.
(Ⅲ)X的取值为0,1,2,
 ,
, ,
,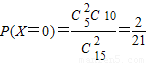 .
.
X的分布列为:
数学期望 .
.
点评:正确理解茎叶图、相互独立事件的概率计算公式、超几何分布、随机变量的分布列、数学期望的计算公式、排列与组合的计算公式是解题的关键.
(II)由(I)的分析及相互独立事件的概率计算公式即可得出;
(III)利用超几何分布即可得到分布列,再利用数学期望的计算公式即可得出.
解答:解:(Ⅰ)甲城市空气质量总体较好.
(Ⅱ)甲城市在15天内空气质量类别为优或良的共有10天,任取1天,空气质量类别为优或良的概率为
 ,
,乙城市在15天内空气质量类别为优或良的共有5天,任取1天,空气质量类别为优或良的概率为
 ,
,在15天内任取1天,估计甲、乙两城市空气质量类别均为优或良的概率为
 .
.(Ⅲ)X的取值为0,1,2,
 ,
, ,
,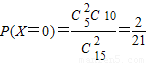 .
.X的分布列为:
| X | 2 | ||
| P |  | 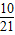 |  |
 .
.点评:正确理解茎叶图、相互独立事件的概率计算公式、超几何分布、随机变量的分布列、数学期望的计算公式、排列与组合的计算公式是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012•佛山二模)空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
(2012•佛山二模)空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
 (2013•延庆县一模)空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
(2013•延庆县一模)空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重: (2012•佛山二模)空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,解代表空气污染越严重:
(2012•佛山二模)空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,解代表空气污染越严重: