题目内容
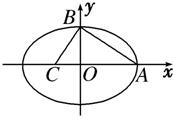 如图,A、B、C分别为
如图,A、B、C分别为| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、1-
| ||||
C、
| ||||
D、
|
分析:由题意知|AC|2=|AB|2+|BC|2,即(a+c)2=a2+2b2+c2,由此可以推导出该椭圆的离心率.
解答:解:|AB|2=a2+b2,|BC|2=b2+c2,
|AC|2=(a+c)2.
∵∠ABC=90°,
∴|AC|2=|AB|2+|BC|2,即(a+c)2=a2+2b2+c2,
∴2ac=2b2,即b2=aC、
∴a2-c2=aC、
∴
-
=1,即
-e=1.
解之得e=
,又∵e>0,
∴e=
.
故选A.
|AC|2=(a+c)2.
∵∠ABC=90°,
∴|AC|2=|AB|2+|BC|2,即(a+c)2=a2+2b2+c2,
∴2ac=2b2,即b2=aC、
∴a2-c2=aC、
∴
| a |
| c |
| c |
| a |
| 1 |
| e |
解之得e=
-1±
| ||
| 2 |
∴e=
-1+
| ||
| 2 |
故选A.
点评:本题考查椭圆的基本性质,解题时结合图形效果较好.

练习册系列答案
相关题目
 如图,A、B、C分别为椭圆
如图,A、B、C分别为椭圆 A.
A. =1(a>b>0)的顶点与焦点,若∠ABC=90°,则该椭圆的离心率为 ( )
=1(a>b>0)的顶点与焦点,若∠ABC=90°,则该椭圆的离心率为 ( )
 B.1-
B.1- C.
C. -1 D.
-1 D.
