题目内容
设数列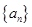 的前
的前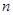 项和为
项和为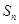 ,且对任意
,且对任意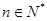 都有:
都有: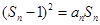 ;
;
(1)求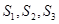 ;
;
(2)猜想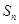 的表达式并证明.
的表达式并证明.
(1)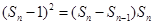
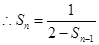 , 又
, 又 ,
,
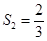 ,
,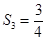 , (2)猜想
, (2)猜想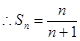 下面用数学归纳法证明(略)
下面用数学归纳法证明(略)
解析试题分析:(1)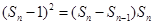
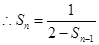 , 又
, 又 ,
,
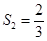 ,
,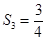 ,
,
(2)猜想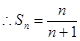 下面用数学归纳法证明:
下面用数学归纳法证明:
1°当n=1时, ,猜想正确;
,猜想正确;
2°假设当n=k时,猜想正确,即 ,
,
那么,n=k+1时,由 ,猜想也成了,
,猜想也成了,
综上知,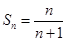 对一切自然数n均成立。
对一切自然数n均成立。
考点:本题主要考查归纳、猜想、证明的推理方法,数学归纳法。
点评:中档题,涉及数列中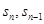 的关系,确定数列的特征,往往要建立两式,相减或相除等。利用数学归纳法证明问题,要注意其步骤规范,做好“两步一结”。
的关系,确定数列的特征,往往要建立两式,相减或相除等。利用数学归纳法证明问题,要注意其步骤规范,做好“两步一结”。

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
已知复数 ,则
,则  ( )
( )
A. | B.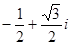 | C. | D. |
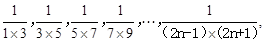 计算
计算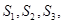 由此推测出
由此推测出 的计算公式,并用数学归纳法证明.
的计算公式,并用数学归纳法证明.
 的值.
的值. ,把
,把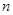 表示
表示 ,当
,当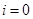 时,
时,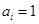 ;当
;当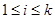 时,
时,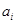 为0或1. 记
为0或1. 记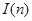 为上述表示中
为上述表示中 ,
,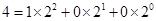 ,
, ,
,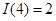 ),若
),若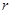 ,
,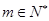 ,
,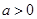 ,则(1)
,则(1)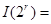 .
.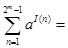 .
.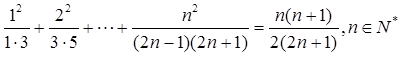
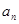 }满足
}满足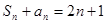 ,
,  ,并推测
,并推测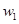 、
、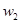 ,定义
,定义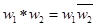 ,其中
,其中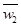 是
是 、
、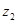 、
、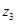 ,有如下四个命题:
,有如下四个命题: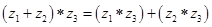 ;
;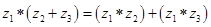 ;
;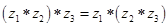 ;
;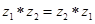 .
.